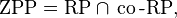Las Vegas algorithm
In computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. In other words, a Las Vegas algorithm does not gamble with the correctness of the result; it gambles only with the resources used for the computation. A simple example is randomized quicksort, where the pivot is chosen randomly, but the result is always sorted. The usual definition of a Las Vegas algorithm includes the restriction that the expected run time always be finite, when the expectation is carried out over the space of random information, or entropy, used in the algorithm. An alternative definition requires that a Las Vegas algorithm always terminate (be effective), but it may output a symbol not part of the solution space to indicate failure in finding a solution.[1]
Las Vegas algorithms were introduced by László Babai in 1979, in the context of the graph isomorphism problem, as a stronger version of Monte Carlo algorithms.[2][3][4] Las Vegas algorithms can be used in situations where the number of possible solutions is relatively limited, and where verifying the correctness of a candidate solution is relatively easy while actually calculating the solution is complex.
The name refers to the city of Las Vegas, Nevada, which is well known within the United States as an icon of gambling.
Complexity class
The complexity class of decision problems that have Las Vegas algorithms with expected polynomial runtime is ZPP.
It turns out that
which is intimately connected with the way Las Vegas algorithms are sometimes constructed. Namely the class RP consists of all decision problems for which a randomized polynomial-time algorithm exists that always answers correctly when the correct answer is "no", but is allowed to be wrong with a certain probability bounded away from one when the answer is "yes". When such an algorithm exists for both a problem and its complement (with the answers "yes" and "no" swapped), the two algorithms can be run simultaneously and repeatedly: run each for a constant number of steps, taking turns, until one of them returns a definitive answer. This is the standard way to construct a Las Vegas algorithm that runs in expected polynomial time. Note that in general there is no worst case upper bound on the run time of a Las Vegas algorithm.
Relation to Monte Carlo algorithms
Las Vegas algorithms can be contrasted with Monte Carlo algorithms, in which the resources used are bounded but the answer is not guaranteed to always be correct. By an application of Markov's inequality, a Las Vegas algorithm can be converted into a Monte Carlo algorithm via early termination.
See also
Notes
- ↑ Steven D. Galbraith (2012). Mathematics of Public Key Cryptography. Cambridge University Press. p. 16. ISBN 978-1-107-01392-6.
- ↑ László Babai, Monte-Carlo algorithms in graph isomorphism testing, Université de Montréal, D.M.S. No. 79-10.
- ↑ Leonid Levin, The Tale of One-way Functions, Problems of Information Transmission, vol. 39 (2003), 92-103.
- ↑ Dan Grundy, Concepts and Calculation in Cryptography, University of Kent, Ph.D. thesis, 2008
References
- Algorithms and Theory of Computation Handbook, CRC Press LLC, 1999, "Las Vegas algorithm", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 17 July 2006. (accessed May 09, 2009) Available from: