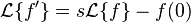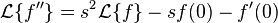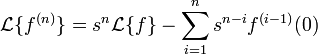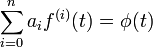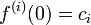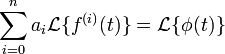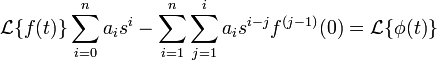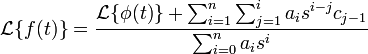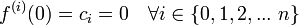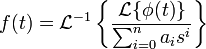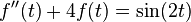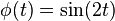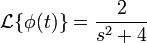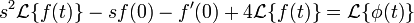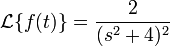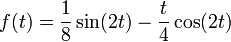Laplace transform applied to differential equations

The Laplace transform is a powerful integral transform used to switch a function from the time domain to the s-domain. The Laplace transform can be used in some cases to solve linear differential equations with given initial conditions.

First consider the following property of the Laplace transform:

\mathcal{L}\{f'\}=s\mathcal{L}\{f\}-f(0)
\mathcal{L}\{f''\}=s^2\mathcal{L}\{f\}-sf(0)-f'(0)

One can prove by induction that

\mathcal{L}\{f^{(n)}\}=s^n\mathcal{L}\{f\}-\sum_{i=1}^{n}s^{n-i}f^{(i-1)}(0)

Now we consider the following differential equation:

\sum_{i=0}^{n}a_if^{(i)}(t)=\phi(t)

with given initial conditions

f^{(i)}(0)=c_i

Using the linearity of the Laplace transform it is equivalent to rewrite the equation as

\sum_{i=0}^{n}a_i\mathcal{L}\{f^{(i)}(t)\}=\mathcal{L}\{\phi(t)\}

obtaining

\mathcal{L}\{f(t)\}\sum_{i=0}^{n}a_is^i-\sum_{i=1}^{n}\sum_{j=1}^{i}a_is^{i-j}f^{(j-1)}(0)=\mathcal{L}\{\phi(t)\}

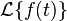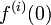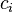Solving the equation for \mathcal{L}\{f(t)\} and substituting f^{(i)}(0) with c_i one obtains

\mathcal{L}\{f(t)\}=\frac{\mathcal{L}\{\phi(t)\}+\sum_{i=1}^{n}\sum_{j=1}^{i}a_is^{i-j}c_{j-1}}{\sum_{i=0}^{n}a_is^i}

The solution for f(t) is obtained by applying the inverse Laplace transform to 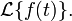\mathcal{L}\{f(t)\}.

Note that if the initial conditions are all zero, i.e.

f^{(i)}(0)=c_i=0\quad\forall i\in\{0,1,2,...\ n\}

then the formula simplifies to

f(t)=\mathcal{L}^{-1}\left\{{\mathcal{L}\{\phi(t)\}\over\sum_{i=0}^{n}a_is^i}\right\}

An example

We want to solve

f''(t)+4f(t)=\sin(2t)

with initial conditions f(0) = 0 and f′(0)=0.

We note that

\phi(t)=\sin(2t)

and we get

\mathcal{L}\{\phi(t)\}=\frac{2}{s^2+4}

The equation is then equivalent to

s^2\mathcal{L}\{f(t)\}-sf(0)-f'(0)+4\mathcal{L}\{f(t)\}=\mathcal{L}\{\phi(t)\}

We deduce

\mathcal{L}\{f(t)\}=\frac{2}{(s^2+4)^2}

Now we apply the Laplace inverse transform to get

f(t)=\frac{1}{8}\sin(2t)-\frac{t}{4}\cos(2t)

Bibliography