Language identification in the limit

Language identification in the limit is a formal model for inductive inference. It was introduced by E. Mark Gold in his paper with the same title ^[1] In this model, a learner is provided with presentation (i.e. strings) of some formal language. The learning is seen as an infinite process. Each time an element of the presentation is read the learner should provide a representation (e.g. a formal grammar) for the language. It is said that a learner can identify in the limit a class of languages if given any presentation of any language in the class the learner will produce only a finite number of wrong representations, and therefore converge on the correct representation in a finite number of steps, without however necessarily being able to announce its correctness since a counterexample to that representation could appear as an element arbitrarily long after.

Gold defined two types of presentations:

Text (positive information): an enumeration of all strings the language consists of.
Complete presentation (positive and negative information): an enumeration of all possible strings, each with a label indicating if the string belongs to the language or not.

Learnability

This model is an early attempt to formally capture the notion of learnability. Gold's paper^[2] introduces for contrast the stronger models

Finite identification (where the learner has to announce correctness after a finite number of steps), and
Fixed-time identification (where correctness has to be reached after an apriori-specified number of steps).

A weaker formal model of learnability is the Probably approximately correct learning (PAC) model, introduced by Leslie Valiant in 1984.

Examples

Example 4
	Teacher	Learner's
		Guess	Query
0.			abab
1.	yes	abab	baba
2.	yes	a^(ba)^b^*	aa
3.	no	(ab)^(ba)^(ab)^(ba)^	bababa
4.	yes	(ab+ba)^*	babb
5.	no	(ab+ba)^*	baaa
	...	...

Example 3
	Teacher	Learner
1.	abab	abab
2.	baba	a^(ba)^b^*
3.	aa	(ab)^(ba)^(ab)^(ba)^
4.	bababa	(ab+ba)^*
5.	~~babb~~	(ab+ba)^*
6.	~~baaa~~	(ab+ba)^*
7.	ε	(ab+ba)^*
	...	...

Example 2
	Teacher	Learner
1.	abab	abab
2.	ba	abab+ba
3.	baba	abab+ba+baba
4.	ba	abab+ba+baba
5.	baba	abab+ba+baba
6.	abab	abab+ba+baba
7.	ε	abab+ba+baba+ε
	...	...

Example 1
	Teacher	Learner
1.	abab	abab
2.	baba	abab+baba
3.	baabab	(b+ε)(ab)^*
4.	baabab	(b+ε)(ab)^+baabab*
5.	abbaabba	(ab)^(ba)^(ab)^(ba)^
6.	baabbaab	(ab+ba)^*
7.	bababa	(ab+ba)^*
	...	...

It is instructive to look at concrete examples of learning sessions the definition of identification in the limit speaks about.

Example 1: fictitious session to learn a regular language L over the alphabet {a,b} from text presentation. In each step, the teacher gives a string belonging to L, and the learner answers a guess for L, encoded as a regular expression. In step 3, the learner's guess is not consistent with the strings seen so far; in step 4, the teacher gives a string repeatedly. After step 6, the learner sticks to the regular expression (ab+ba)^*. If this happens to be a description of the language L the teacher has in mind, it is said that the learner has learned that language. If a computer program for the learner's role would exist that was able to successfully learn each regular language, that class of languages would be identifiable in the limit. Gold has shown that this is not the case.^[3]
Example 2: a particular learning algorithm always guessing L to be just the union of all strings seen so far. If L is a finite language, the learner will eventually guess it correctly, however, without being able to tell when. Although the guess didn't change during step 3 to 6, the learner couldn't be sure to be correct. Gold has shown that the class of finite languages is identifibale in the limit.;^[4] however, this class is neither finitely nor fixed-time identifiable.
Example 3: learning from complete presentation by telling. In each step, the teacher gives a string and tells whether it belongs to L (green) or not (~~red, striked-out~~). Each possible string is eventually classified in this way by the teacher.
Example 4: learning from complete presentation by request. The learner gives a query string, the teacher tell whether it belongs to L (yes) or not (no); the learner then gives a guess for L, followed by the next query string. In this example, the learner happens to query in each step just the same string as given by the teacher in example 3. In general, Gold has shown that each language class identifiable in the request-presentation setting is also identifiable in the telling-presentation setting,^[5] since the learner, instead of querying a string, just needs to wait until it is eventually given by the teacher.

Learnability characterization

Dana Angluin gave the characterizations of learnability from text (positive information) in a 1980 paper. ^[6] If a learner is required to be effective, then an indexed class of recursive languages is learnable in the limit if there is an effective procedure that uniformly enumerates tell-tales for each language in the class (Condition 1).^[7] It is not hard to see that if we allow an ideal learner (i.e., an arbitrary function), then an indexed class of languages is learnable in the limit if each language in the class has a tell-tale (Condition 2).^[8]

Language classes learnable in the limit

Dividing lines between identifiable and nonidentifiable language classes^[9]
Learnability model	Class of languages
Anomalous text presentation^{[note 1]}
	Recursively enumerable
	Recursive
Complete presentation
	Primitive recursive^{[note 2]}
	Context-sensitive
	Context-free
	Regular
	Superfinite^{[note 3]}
Normal text presentation^{[note 4]}
	Finite
	Singleton^{[note 5]}

The table shows which language classes are identifiable in the limit in which learning model. On the right hand side, each language class is a super class of all lower classes. Each learning model (i.e. type of presentation) can identify in the limit all classes below it. In particular, the class of finite languages is identifiable in the limit by text presentation (cf. Example 2 above), while the class of regular languages is not.

Pattern Languages, introduced by Dana Angluin in another 1980 paper, ^[10] are also identifiable by normal text presentation; they are omitted in the table, since they are above the singleton and below the primitive recursive language class, but incomparable to the classes in between.^{[note 6]}

Sufficient conditions for learnability

Condition 1 in Angluin's paper^[7] is not always easy to verify. Therefore, people come up with various sufficient conditions for the learnability of a language class. See also Induction of regular languages for learnable subclasses of regular languages.

Finite thickness

A class of languages has finite thickness if every non-empty set of strings is contained in at most finitely many languages of the class. This is exactly Condition 3 in Angluin's paper.^[11] Angluin showed that if a class of recursive languages has finite thickness, then it is learnable in the limit.^[12]

A class with finite thickness certainly satisfies MEF-condition and MFF-condition; in other words, finite thickness implies M-finite thickness.^[13]

Finite elasticity

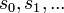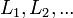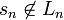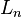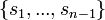A class of languages is said to have finite elasticity if for every infinite sequence of strings $s_0, s_1, ...$ and every infinite sequence of languages in the class $L_1, L_2, ...$ , there exists a finite number n such that $s_n\not\in L_n$ implies $L_n$ is inconsistent with $\{s_1,...,s_{n-1}\}$ .

It is shown that a class of recursively enumerable languages is learnable in the limit if it has finite elasticity.

Other concepts

Infinite cross property

A language L has infinite cross property within a class of languages 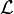$\mathcal{L}$ if there is an infinite sequence 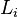$L_i$ of distinct languages in 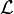$\mathcal{L}$ and a sequence of finite subset 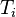$T_i$ such that:

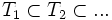$T_1 \sub T_2\sub ...$ ,
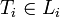$T_i \in L_i$ ,
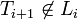$T_{i+1}\not\in L_i$ , and
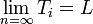$\lim_{n=\infty}T_i=L$ .

Note that L is not necessarily a member of the class of language.

It is not hard to see that if there is a language with infinite cross property within a class of languages, then that class of languages has infinite elasticity.

Relations between concepts

Finite thickness implies finite elasticity;^[13]^[14] the converse is not true.
Finite elasticity and conservatively learnable implies the existence of a mind change bound.
Finite elasticity and M-finite thickness implies the existence of a mind change bound. However, M-finite thickness alone does not imply the existence of a mind change bound; neither does the existence of a mind change bound imply M-finite thickness.
Existence of a mind change bound implies learnability; the converse is not true.
If we allow for noncomputable learners, then finite elasticity implies the existence of a mind change bound; the converse is not true.
If there is no accumulation order for a class of languages, then there is a language (not necessarily in the class) that has infinite cross property within the class, which in turn implies infinite elasticity of the class.

Open questions

If a countable class of recursive languages has a mind change bound for noncomputable learners, does the class also have a mind change bound for computable learners, or is the class unlearnable by a computable learner?

Notes

↑ i.e. text presentation, where the string given by the teacher is a primitive recursive function of the current step number, and the learner encodes a language guess as a program that enumerates the language
↑ i.e. the class of languages that are decidable by primitive recursive functions
↑ i.e. containing all finite languages and at least one infinite one
↑ i.e. text presentation, expect for the anomalous text presentation setting
↑ i.e. the class of languages consisting of a single string (they are mentioned here only as a common lower bound to finite languages and pattern languages)
↑ incomparable to regular and to context-free language class: Theorem 3.10, p.53

References

↑ Gold, E. Mark (1967). "Language identification in the limit". Information and Control 10 (5): 447–474. doi:10.1016/S0019-9958(67)91165-5.
↑ p.457
↑ Theorem I.8,I.9, p.470-471
↑ Theorem I.6, p.469
↑ Theorem I.3, p.467
↑ Dana Angluin (1980). "Inductive Inference of Formal Languages from Positive Data". Information and Control 45: 117–135. doi:10.1016/S0019-9958(80)90285-5.
↑ 7.0 7.1 p.121 top
↑ p.123 top
↑ Table 1, p.452, in (Gold 1967)
↑ Dana Angluin (1980). "Finding Patterns Common to a Set of Strings". Journal of Computer and System Sciences 21: 46–62. doi:10.1016/0022-0000(80)90041-0.
↑ p.123 mid
↑ p.123 bot, Corollary 2
↑ 13.0 13.1 Andris Ambainis, Sanjay Jain, Arun Sharma (1997). "Ordinal mind change complexity of language identification". Computational Learning Theory. LNCS 1208. Springer. pp. 301–315. ; here: Proof of Corollary 29
↑ Wright, Keith (1989) "Identification of Unions of Languages Drawn from an Identifiable Class". Proc. 2nd Workwhop on Computational Learning Theory, 328-333; with correction in: Motoki, Shinohara, and Wright (1991) "The correct definition of finite elasiticity: corrigendum to identification of unions", Proc. 4th Workshop on Computational Learing Theory, 375-375