Langley’s Adventitious Angles

Langley’s Adventitious Angles

Langley’s Adventitious Angles is a mathematical problem posed by Edward Mann Langley in the Mathematical Gazette in 1922.[1][2]

The problem

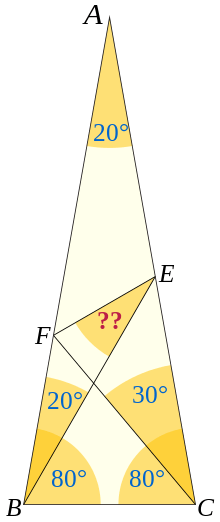
In its original form the problem was as follows: ABC is an isosceles triangle. B = C = 80 degrees. CF at 30 degrees to AC cuts AB in F. BE at 20 degrees to AB cuts AC in E. Prove angle BEF = 30 degrees.[2][3]

Solution

A solution was developed by James Mercer in 1923: Draw BG at 20 degrees to BC cutting CA in G. Then angle GBF = 60 degrees and angles BGC and BCG are 80 degrees. So BC = BG. Also angle BCF = angle BFC = 50 degrees, so BF = BG and triangle BFG is equilateral. But angle GBE = 40 degrees = angle BEG, so BG = GE = GF. And angle FGE = 40 degrees, hence GEF = 70 degrees and BEF = 30 degrees.[2]

Generalization

A quadrilateral such as BCEF in which the angles formed by all triples of vertices are rational multiples of π is called an adventitious quadrangle. Several constructions for other adventitious quadrangles, beyond the one appearing in Langley's puzzle, are known. They form several infinite families and an additional set of sporadic examples.[4]

References

  1. ↑ Langley, E. M. (1922), "Problem 644", The Mathematical Gazette 11: 173.
  2. ↑ 2.0 2.1 2.2 Darling, David (2004), The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, p. 180.
  3. ↑ Tripp, Colin (1975), "Adventitious angles", The Mathematical Gazette 59: 98–106, JSTOR 3616644.
  4. ↑ Rigby, J. F. (1978), "Adventitious quadrangles: a geometrical approach", The Mathematical Gazette 62 (421): 183–191, doi:10.2307/3616687, MR 513855.

External links