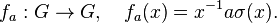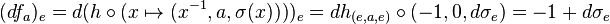Lang's theorem

In algebraic geometry, Lang's theorem, introduced by Serge Lang, states: if G is a connected smooth algebraic group over a finite field 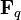$\mathbf{F}_q$ , then, writing 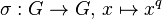$\sigma: G \to G, \, x \mapsto x^q$ for the Frobenius, the morphism of varieties

G \to G, \, x \mapsto x^{-1} \sigma(x)

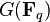is surjective. Note that the kernel of this map (i.e., $G = G(\overline{\mathbf{F}_q}) \to G(\overline{\mathbf{F}_q})$ ) is precisely $G(\mathbf{F}_q)$ .

The theorem implies that 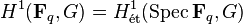$H^1(\mathbf{F}_q, G) = H_{\mathrm{\acute{e}t}}^1(\operatorname{Spec}\mathbf{F}_q, G)$ vanishes,^[1] and, consequently, any G-bundle on 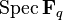$\operatorname{Spec} \mathbf{F}_q$ is isomorphic to the trivial one. Also, the theorem plays a basic role in the theory of finite groups of Lie type.

It is not necessary that G is affine. Thus, the theorem also applies to abelian varieties (e.g., elliptic curves.) In fact, this application was Lang's initial motivation. If G is affine, the Frobenius $\sigma$ may be replaced by any surjective map with finitely many fixed points (see below for the precise statement.)

The proof (given below) actually goes through for any $\sigma$ that induces a nilpotent operator on the Lie algebra of G.^[2]

The Lang–Steinberg theorem

Steinberg (1968) gave a useful improvement to the theorem.

Suppose that F is an endomorphism of an algebraic group G. The Lang map is the map from G to G taking g to g⁻¹F(g).

The Lang–Steinberg theorem states^[3] that if F is surjective and has a finite number of fixed points, and G is a connected affine algebraic group over an algebraically closed field, then the Lang map is surjective.

Proof of Lang's theorem

Define:

f_a: G \to G, \quad f_a(x) = x^{-1}a\sigma(x).

Then (identifying the tangent space at a with the tangent space at the identity element) we have:

(d f_a)_e = d(h \circ (x \mapsto (x^{-1}, a, \sigma(x))))_e = dh_{(e, a, e)} \circ (-1, 0, d\sigma_e) = -1 + d \sigma_e

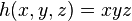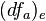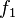where $h(x, y, z) = xyz$ . It follows $(d f_a)_e$ is bijective since the differential of the Frobenius $\sigma$ vanishes. Since $f_a(bx) = f_{f_a(b)}(x)$ , we also see that $(df_a)_b$ is bijective for any b.^[4] Let X be the closure of the image of $f_1$ . The smooth points of X form an open dense subset; thus, there is some b in G such that 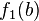$f_1(b)$ is a smooth point of X. Since the tangent space to X at 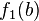$f_1(b)$ and the tangent space to G at b have the same dimension, it follows that X and G have the same dimension, since G is smooth. Since G is connected, the image of 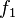$f_1$ then contains an open dense subset U of G. Now, given an arbitrary element a in G, by the same reasoning, the image of 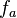$f_a$ contains an open dense subset V of G. The intersection 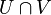$U \cap V$ is then nonempty but then this implies a is in the image of $f_1$ .

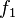Notes

↑ This is "unwinding definition". Here, $H^1(\mathbf{F}_q, G) = H^1(\operatorname{Gal}(\overline{\mathbf{F}_q}/\mathbf{F}_q), G(\overline{\mathbf{F}_q}))$ is Galois cohomology; cf. Milne, Class field theory.
↑ Springer 1998, Exercise 4.4.18.
↑ Steinberg 1968, Theorem 10.1
↑ This implies that 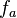$f_a$ is étale.

References

T.A. Springer, "Linear algebraic groups", 2nd ed. 1998.
Lang, Serge (1956), "Algebraic groups over finite fields", American Journal of Mathematics 78: 555–563, doi:10.2307/2372673, ISSN 0002-9327, MR 0086367
Steinberg, Robert (1968), Endomorphisms of linear algebraic groups, Memoirs of the American Mathematical Society, No. 80, Providence, R.I.: American Mathematical Society, MR 0230728