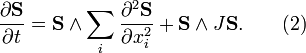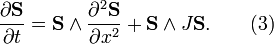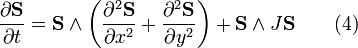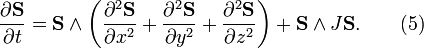Landau–Lifshitz model

For another Landau–Lifshitz equation describing magnetism, see Landau–Lifshitz–Gilbert equation.

In solid-state physics, the Landau–Lifshitz equation (LLE), named for Lev Landau and Evgeny Lifshitz, is a partial differential equation describing time evolution of magnetism in solids, depending on 1 time variable and 1, 2, or 3 space variables.

Landau–Lifshitz equation

The LLE describes an anisotropic magnet. The equation is described in (Faddeev & Takhtajan 2007, chapter 8) as follows: It is an equation for a vector field S, in other words a function on R¹⁺ⁿ taking values in R³. The equation depends on a fixed symmetric 3 by 3 matrix J, usually assumed to be diagonal; that is, $J=\operatorname{diag}(J_{1}, J_{2}, J_{3})$ . It is given by Hamilton's equation of motion for the Hamiltonian

H=\frac{1}{2}\int \left[\sum_i\left(\frac{\partial \mathbf{S}}{\partial x_i}\right)^{2}-J(\mathbf{S})\right]\, dx\qquad (1)

(where J(S) is the quadratic form of J applied to the vector S) which is

\frac{\partial \mathbf{S}}{\partial t} = \mathbf{S}\wedge \sum_i\frac{\partial^2 \mathbf{S}}{\partial x_i^{2}} + \mathbf{S}\wedge J\mathbf{S}.\qquad (2)

In 1+1 dimensions this equation is

\frac{\partial \mathbf{S}}{\partial t} = \mathbf{S}\wedge \frac{\partial^2 \mathbf{S}}{\partial x^{2}} + \mathbf{S}\wedge J\mathbf{S}.\qquad (3)

In 2+1 dimensions this equation takes the form

\frac{\partial \mathbf{S}}{\partial t} = \mathbf{S}\wedge \left(\frac{\partial^2 \mathbf{S}}{\partial x^{2}} + \frac{\partial^2 \mathbf{S}}{\partial y^{2}}\right)+ \mathbf{S}\wedge J\mathbf{S}\qquad (4)

which is the (2+1)-dimensional LLE. For the (3+1)-dimensional case LLE looks like

\frac{\partial \mathbf{S}}{\partial t} = \mathbf{S}\wedge \left(\frac{\partial^2 \mathbf{S}}{\partial x^{2}} + \frac{\partial^2 \mathbf{S}}{\partial y^{2}}+\frac{\partial^2 \mathbf{S}}{\partial z^{2}}\right)+ \mathbf{S}\wedge J\mathbf{S}.\qquad (5)

Integrable reductions

In general case LLE (2) is nonintegrable. But it admits the two integrable reductions:

a) in the 1+1 dimensions, that is Eq. (3), it is integrable

b) when

J=0

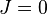. In this case the (1+1)-dimensional LLE (3) turns into the continuous classical Heisenberg ferromagnet equation (see e.g. Heisenberg model (classical)) which is already integrable.

References

Faddeev, Ludwig D.; Takhtajan, Leon A. (2007), Hamiltonian methods in the theory of solitons, Classics in Mathematics, Berlin: Springer, pp. x+592, ISBN 978-3-540-69843-2, MR 2348643
Guo, Boling; Ding, Shijin (2008), Landau-Lifshitz Equations, Frontiers of Research With the Chinese Academy of Sciences, World Scientific Publishing Company, ISBN 978-981-277-875-8
Kosevich A.M., Ivanov B.A., Kovalev A.S. Nonlinear magnetization waves. Dynamical and topological solitons. – Kiev: Naukova Dumka, 1988. – 192 p.

Landau–Lifshitz model

Landau–Lifshitz equation

Integrable reductions

See also

References