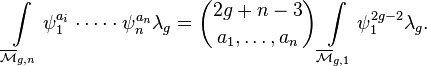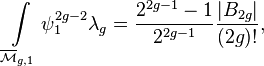λg conjecture

In algebraic geometry, the 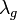$\lambda_g$ -conjecture gives a particularly simple formula for certain integrals on the Deligne–Mumford compactification 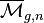$\overline{\mathcal M}_{g, n}$ of the moduli space of curves with marked points. It was first found as a consequence of the Virasoro conjecture by E. Getzler and R. Pandharipande (1998). Later, it was proven by C. Faber and R. Pandharipande (2003) using virtual localization in Gromov–Witten theory. It is named after the factor of 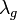$\lambda_g$ , the gth Chern class of the Hodge bundle, appearing in its integrand. The other factor is a monomial in the 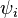$\psi_i$ , the first Chern classes of the n cotangent line bundles, as in Witten's conjecture.

Let a₁, ..., a_n be positive integers whose sum is 2g − 3 + n. Then the 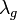$\lambda_g$ -formula says that

\int\limits_{\overline{\mathcal M}_{g, n}} \psi_1^{a_i} \cdot \dots \cdot \psi_n^{a_n}\lambda_g = \binom{2g + n - 3}{a_1, \dots, a_n} \int\limits_{\overline{\mathcal M}_{g, 1}} \psi_1^{2g - 2}\lambda_g.

Together with the formula

\int\limits_{\overline{\mathcal M}_{g, 1}} \psi_1^{2g - 2}\lambda_g = \frac{2^{2g - 1} - 1}{2^{2g - 1}} \frac{|B_{2g}|}{(2g)!},

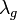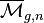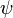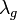where the B_2g are Bernoulli numbers, therefore the $\lambda_g$ -formula gives a way to calculate all integrals on $\overline{\mathcal M}_{g, n}$ involving products in $\psi$ -classes and a factor of $\lambda_g$ .

References

Pandharipande, E.; Pandharipande, R. (1998), "Virasoro constraints and the Chern classes of the Hodge bundle", Nuclear Phys. B530 (3): 701–714, arXiv:math.AG/9805114, Bibcode:1998NuPhB.530..701G, doi:10.1016/S0550-3213(98)00517-3
Faber, C.; Pandharipande, R. (2003), "Hodge integrals, partition matrices, and the 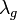$\lambda_g$ conjecture", Ann. Of Math. (2) 157 (1): 97–124, arXiv:math.AG/9805114, doi:10.4007/annals.2003.157.97