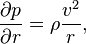Lamb–Oseen vortex
In fluid dynamics, the Lamb–Oseen vortex models a line vortex that decays due to viscosity. This vortex is named after Horace Lamb and Carl Wilhelm Oseen.[1]
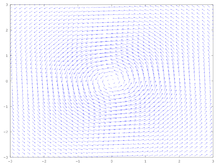
Vector plot of the Lamb-Oseen vortex
The mathematical model for the flow velocity in the circumferential 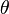 –direction in the Lamb–Oseen vortex is:
–direction in the Lamb–Oseen vortex is:
with
 = radius,
= radius,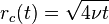 = core radius of vortex,
= core radius of vortex,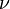 = viscosity, and
= viscosity, and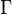 = circulation contained in the vortex.
= circulation contained in the vortex.
The radial velocity is equal to zero.
An alternative definition is to use the peak tangential velocity of the vortex rather than the total circulation
where 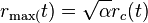 is the radius at which
is the radius at which 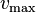 is
attained, and the number α = 1.25643, see Devenport et al.[2]
is
attained, and the number α = 1.25643, see Devenport et al.[2]
The pressure field simply ensures the vortex rotates in the circumferential direction, providing the centripetal force
where ρ is the constant density[3]
References
- ↑ Saffman, P. G.; Ablowitz, Mark J.; J. Hinch, E.; Ockendon, J. R.; Olver, Peter J. (1992). Vortex dynamics. Cambridge: Cambridge University Press. ISBN 0-521-47739-5. p. 253.
- ↑ W.J. Devenport, M.C. Rife, S.I. Liapis and G.J. Follin (1996). "The structure and development of a wing-tip vortex". Journal of Fluid Mechanics 312: 67–106. Bibcode:1996JFM...312...67D. doi:10.1017/S0022112096001929.
- ↑ G.K. Batchelor (1967). An Introduction to Fluid Dynamics. Cambridge University Press.
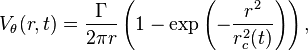
![V_\theta\left( r \right) =
V_{\theta \max} \left( 1 + \frac{1}{2\alpha} \right)
\frac{r_\max}{r}
\left[ 1 - \exp \left( - \alpha \frac{r^2}{r_\max^2} \right)
\right],](../I/m/81c38524d052cf16bcd25866a00c5b8a.png)