Lagrange's theorem (number theory)
In number theory, Lagrange's theorem is a statement named after Joseph-Louis Lagrange about how frequently a polynomial over the integers may evaluate to a multiple of a fixed prime. More precisely, it states that if p is a prime number and ![\textstyle f(x) \in \mathbb{Z}[x]](../I/m/0eb262ae7f62b22af9312e1848a17a8f.png) is a polynomial with integer coefficients, then either:
is a polynomial with integer coefficients, then either:
- every coefficient of f(x) is divisible by p, or
-
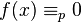 has at most deg f(x) incongruent solutions.
has at most deg f(x) incongruent solutions.
Solutions are "incongruent" if they do not differ by a multiple of p. If the modulus is not prime, then it is possible for there to be more than deg f(x) solutions.
A proof of Lagrange's theorem
The two key ideas are the following. Let ![\textstyle g(x) \in (\mathbb{Z}/p)[x]](../I/m/aa7e5be46863f9a9cace92b7506e81eb.png) be the polynomial obtained from
be the polynomial obtained from 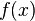 by taking the coefficients
by taking the coefficients 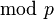 . Now (i)
. Now (i) 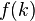 is divisible by
is divisible by  if and only if
if and only if 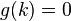 ; (ii)
; (ii) 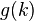 has no more roots than its degree.
has no more roots than its degree.
More rigorously, start by noting that 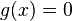 if and only if each coefficient of
if and only if each coefficient of 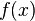 is divisible by
is divisible by  . Assume
. Assume 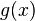 is not 0; its degree is thus well-defined. It's easy to see
is not 0; its degree is thus well-defined. It's easy to see 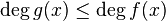 . To prove (i), first note that we can compute
. To prove (i), first note that we can compute 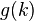 either directly, i.e. by plugging in (the residue class of)
either directly, i.e. by plugging in (the residue class of)  and performing arithmetic in
and performing arithmetic in 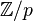 , or by reducing
, or by reducing 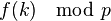 . Hence
. Hence 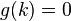 if and only if
if and only if 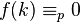 , i.e. if and only if
, i.e. if and only if 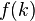 is divisible by
is divisible by  . To prove (ii), note that
. To prove (ii), note that 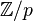 is a field, which is a standard fact; a quick proof is to note that since
is a field, which is a standard fact; a quick proof is to note that since  is prime,
is prime, 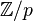 is a finite integral domain, hence is a field. Another standard fact is that a non-zero polynomial over a field has at most as many roots as its degree; this follows from the division algorithm.
is a finite integral domain, hence is a field. Another standard fact is that a non-zero polynomial over a field has at most as many roots as its degree; this follows from the division algorithm.
Finally, note that two solutions 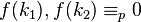 are incongruent if and only if
are incongruent if and only if 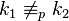 . Putting it all together: the number of incongruent solutions by (i) is the same as the number of roots of
. Putting it all together: the number of incongruent solutions by (i) is the same as the number of roots of 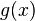 , which by (ii) is at most
, which by (ii) is at most 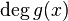 , which is at most
, which is at most 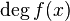 .
.
References
- LeVeque, William J. (2002) [1956]. Topics in Number Theory, Volumes I and II. New York: Dover Publications. p. 42. ISBN 978-0-486-42539-9. Zbl 1009.11001.
- Tattersall, James J. (2005). Elementary Number Theory in Nine Chapters (2nd ed.). Cambridge University Press. p. 198. ISBN 0-521-85014-2. Zbl 1071.11002.