Ladder graph
| Ladder graph | |
|---|---|
|
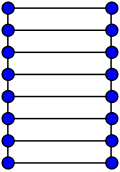
The ladder graph L8. | |
| Vertices | 2n |
| Edges | n+2(n-1) |
| Chromatic number | 2 |
| Chromatic index |
3 for n>2 2 for n=2 1 for n=1 |
| Properties |
Unit distance Hamiltonian Planar Bipartite |
| Notation | Ln |
In the mathematical field of graph theory, the ladder graph Ln is a planar undirected graph with 2n vertices and n+2(n-1) edges.[1]
The ladder graph can be obtained as the Cartesian product of two path graphs, one of which has only one edge: Ln,1 = Pn × P1.[2][3] Adding two more crossed edges connecting the four degree-two vertices of a ladder graph produces a cubic graph, the Möbius ladder.
By construction, the ladder graph Ln is isomorphic to the grid graph G2,n and looks like a ladder with n rungs. It is Hamiltonian with girth 4 (if n>1) and chromatic index 3 (if n>2).
The chromatic number of the ladder graph is 2 and its chromatic polynomial is 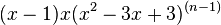 .
.
Gallery

The ladder graphs L1, L2, L3, L4 and L5.
-
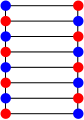
The chromatic number of the ladder graph is 2.
References
- ↑ Weisstein, Eric W., "Ladder Graph", MathWorld.
- ↑ Hosoya, H. and Harary, F. "On the Matching Properties of Three Fence Graphs." J. Math. Chem. 12, 211-218, 1993.
- ↑ Noy, M. and Ribó, A. "Recursively Constructible Families of Graphs." Adv. Appl. Math. 32, 350-363, 2004.