LF-space
In mathematics, an LF-space is a topological vector space V that is a locally convex inductive limit of a countable inductive system  of Fréchet spaces. This means that V is a direct limit of the system
of Fréchet spaces. This means that V is a direct limit of the system  in the category of locally convex topological vector spaces and each
in the category of locally convex topological vector spaces and each 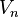 is a Fréchet space.
is a Fréchet space.
Some authors restrict the term LF-space to mean that V is a strict locally convex inductive limit, which means that the topology induced on 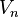 by
by 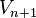 is identical to the original topology on
is identical to the original topology on 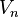 .[1]
.[1]
The topology on V can be described by specifying that an absolutely convex subset U is a neighborhood of 0 if and only if  is an absolutely convex neighborhood of 0 in
is an absolutely convex neighborhood of 0 in 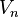 for every n.
for every n.
Properties
An LF-space is barrelled and bornological (and thus ultrabornological).
Examples
A typical example of an LF-space is, 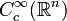 , the space of all infinitely differentiable functions on
, the space of all infinitely differentiable functions on 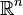 with compact support. The LF-space structure is obtained by considering a sequence of compact sets
with compact support. The LF-space structure is obtained by considering a sequence of compact sets 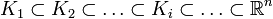 with
with  and for all i,
and for all i, 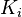 is a subset of the interior of
is a subset of the interior of 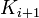 . Such a sequence could be the balls of radius i centered at the origin. The space
. Such a sequence could be the balls of radius i centered at the origin. The space  of infinitely differentiable functions on
of infinitely differentiable functions on 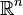 with compact support contained in
with compact support contained in 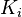 has a natural Fréchet space structure and
has a natural Fréchet space structure and 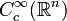 inherits its LF-space structure as described above. The LF-space topology does not depend on the particular sequence of compact sets
inherits its LF-space structure as described above. The LF-space topology does not depend on the particular sequence of compact sets 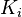 .
.
With this LF-space structure,  is known as the space of test functions, of fundamental importance in the theory of distributions.
is known as the space of test functions, of fundamental importance in the theory of distributions.
References
- Treves, François (1967), Topological Vector Spaces, Distributions and Kernels, Academic Press, pp. 126 ff.
| ||||||||||||||||||||||||||||||||||