L-stability

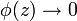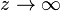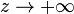L-stability is a special case of A-stability, a property of Runge–Kutta methods for solving ordinary differential equations. A method is L-stable if it is A-stable and $\phi(z) \to 0$ as $z \to \infty$ , where $\phi$ is the stability function of the method (the stability function of a Runge–Kutta method is a rational function and thus the limit as $z \to +\infty$ is the same as the limit as 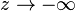$z \to -\infty$ ). L-stable methods are in general very good at integrating stiff equations.

References

Hairer, Ernst; Wanner, Gerhard (1996), Solving ordinary differential equations II: Stiff and differential-algebraic problems (second ed.), Berlin: Springer-Verlag, section IV.3, ISBN 978-3-540-60452-5 .