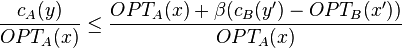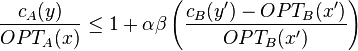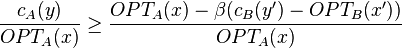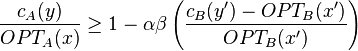L-reduction
In computer science, particularly the study of approximation algorithms, an L-reduction ("linear reduction") is a transformation of optimization problems which linearly preserves approximability features; it is one type of approximation-preserving reduction. L-reductions in studies of approximability of optimization problems play a similar role to that of polynomial reductions in the studies of computational complexity of decision problems.
The term L reduction is sometimes used to refer to log-space reductions, by analogy with the complexity class L, but this is a different concept.
Definition
Let A and B be optimization problems and cA and cB their respective cost functions. A pair of functions f and g is an L-reduction if all of the following conditions are met:
- functions f and g are computable in polynomial time,
- if x is an instance of problem A, then f(x) is an instance of problem B,
- if y' is a solution to f(x), then g(y' ) is a solution to x,
- there exists a positive constant α such that
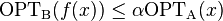 ,
,
- there exists a positive constant β such that for every solution y' to f(x)
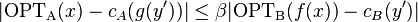 .
.
Properties
Implication of PTAS reduction
An L-reduction from problem A to problem B implies an AP-reduction when A and B are minimization problems and a PTAS reduction when A and B are maximization problems. In both cases, when B has a PTAS and there is a L-reduction from A to B, then A also has a PTAS.[1][2] This enables the use of L-reduction as a replacement for showing the existence of a PTAS-reduction; Crescenzi has suggested that the more natural formulation of L-reduction is actually more useful in many cases due to ease of usage.[3]
Proof (minimization case)
Let the approximation ratio of B be 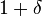 .
Begin with the approximation ratio of A,
.
Begin with the approximation ratio of A, 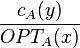 .
We can remove absolute values around the third condition of the L-reduction definition since we know A and B are minimization problems. Substitute that condition to obtain
.
We can remove absolute values around the third condition of the L-reduction definition since we know A and B are minimization problems. Substitute that condition to obtain
Simplifying, and substituting the first condition, we have
But the term in parentheses on the right-hand side actually equals 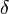 . Thus, the approximation ratio of A is
. Thus, the approximation ratio of A is 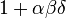 .
.
This meets the conditions for AP-reduction.
Proof (maximization case)
Let the approximation ratio of B be 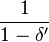 .
Begin with the approximation ratio of A,
.
Begin with the approximation ratio of A, 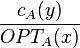 .
We can remove absolute values around the third condition of the L-reduction definition since we know A and B are maximization problems. Substitute that condition to obtain
.
We can remove absolute values around the third condition of the L-reduction definition since we know A and B are maximization problems. Substitute that condition to obtain
Simplifying, and substituting the first condition, we have
But the term in parentheses on the right-hand side actually equals 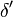 . Thus, the approximation ratio of A is
. Thus, the approximation ratio of A is 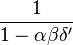 .
.
If 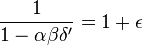 , then
, then 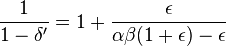 , which meets the requirements for PTAS reduction but not AP-reduction.
, which meets the requirements for PTAS reduction but not AP-reduction.
Other properties
L-reductions also imply P-reduction.[3] One may deduce that L-reductions imply PTAS reductions from this fact and the fact that P-reductions imply PTAS reductions.
L-reductions preserve membership in APX for the minimizing case only, as a result of implying AP-reductions.
Examples
- Dominating set: an example with α = β = 1
- Token reconfiguration: an example with α = 1/5, β = 2
See also
References
- ↑ Kann, Viggo (1992). On the Approximability of NP-complete Optimization Problems. Royal Institute of Technology, Sweden. ISBN 91-7170-082-X.
- ↑ Christos H. Papadimitriou; Mihalis Yannakakis (1988). "Optimization, Approximation, and Complexity Classes". STOC '88: Proceedings of the twentieth annual ACM Symposium on Theory of Computing. doi:10.1145/62212.62233.
- ↑ 3.0 3.1 Crescenzi, Pierluigi (1997). "A Short Guide To Approximation Preserving Reductions". Proceedings of the 12th Annual IEEE Conference on Computational Complexity (Washington, D.C.: IEEE Computer Society): 262–.
- G. Ausiello, P. Crescenzi, G. Gambosi, V. Kann, A. Marchetti-Spaccamela, M. Protasi. Complexity and Approximation. Combinatorial optimization problems and their approximability properties. 1999, Springer. ISBN 3-540-65431-3