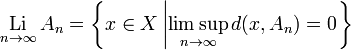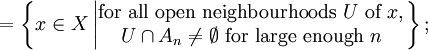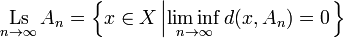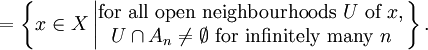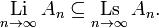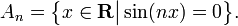Kuratowski convergence

In mathematics, Kuratowski convergence is a notion of convergence for sequences (or, more generally, nets) of compact subsets of metric spaces, named after the Polish mathematician Kazimierz Kuratowski. Intuitively, the Kuratowski limit of a sequence of sets is where the sets "accumulate".

Definitions

Let (X, d) be a metric space, where X is a set and d is the function of distance between points of X.

For any point x ∈ X and any non-empty compact subset A ⊆ X, define the distance between the point and the subset:

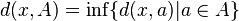d(x, A) = \inf \{ d(x, a) | a \in A \}

For any sequence of such subsets A_n ⊆ X, n ∈ N, the Kuratowski limit inferior (or lower closed limit) of A_n as n → ∞ is

\mathop{\mathrm{Li}}_{n \to \infty} A_{n} = \left\{ x \in X \left| \limsup_{n \to \infty} d(x, A_{n}) = 0 \right. \right\}

= \left\{ x \in X \left| \begin{matrix} \mbox{for all open neighbourhoods } U \mbox{ of } x, \\ U \cap A_{n} \neq \emptyset \mbox{ for large enough } n \end{matrix} \right. \right\};

the Kuratowski limit superior (or upper closed limit) of A_n as n → ∞ is

\mathop{\mathrm{Ls}}_{n \to \infty} A_{n} = \left\{ x \in X \left| \liminf_{n \to \infty} d(x, A_{n}) = 0 \right. \right\}

= \left\{ x \in X \left| \begin{matrix} \mbox{for all open neighbourhoods } U \mbox{ of } x, \\ U \cap A_{n} \neq \emptyset \mbox{ for infinitely many } n \end{matrix} \right. \right\}.

If the Kuratowski limits inferior and superior agree (i.e. are the same subset of X), then their common value is called the Kuratowski limit of the sets A_n as n → ∞ and denoted Lt_n→∞A_n.

The definitions for a general net of compact subsets of X go through mutatis mutandis.

Properties

Although it may seem counter-intuitive that the Kuratowski limit inferior involves the limit superior of the distances, and vice versa, the nomenclature becomes more obvious when one sees that, for any sequence of sets,

\mathop{\mathrm{Li}}_{n \to \infty} A_{n} \subseteq \mathop{\mathrm{Ls}}_{n \to \infty} A_{n}.

I.e. the limit inferior is the smaller set and the limit superior the larger one.

The terms upper and lower closed limit stem from the fact that Li_n→∞A_n and Ls_n→∞A_n are always closed sets in the metric topology on (X, d).

Related Concepts

For metric spaces X we have the following:

Kuratowski convergence coincides with convergence in Fell topology.
Kuratowski convergence is weaker than convergence in Vietoris topology.
Kuratowski convergence is weaker than convergence in Hausdorff metric.
For compact metric spaces X, Kuratowski convergence coincides with both convergence in Hausdorff metric and Vietoris topology.

Examples

Let A_n be the zero set of sin(nx) as a function of x from R to itself

A_{n} = \big\{ x \in \mathbf{R} \big| \sin (n x) = 0 \big\}.

Then A_n converges in the Kuratowski sense to the whole real line R. Observe that in this case, the A_n do not need to be compact.

References