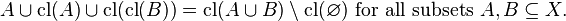Kuratowski closure axioms

In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms that can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition. They were first introduced by Kazimierz Kuratowski.^[1]

A similar set of axioms can be used to define a topological structure using only the dual notion of interior operator.

Definition

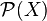Let $X$ be a set and $\mathcal{P}(X)$ its power set.
A Kuratowski Closure Operator is an assignment 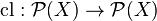$\operatorname{cl}:\mathcal{P}(X) \to \mathcal{P}(X)$ with the following properties:^[2]

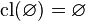$\operatorname{cl}(\varnothing) = \varnothing$ (Preservation of Nullary Union)
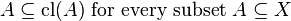$A \subseteq \operatorname{cl}(A) \text{ for every subset }A \subseteq X$ (Extensivity)
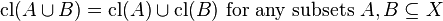$\operatorname{cl}(A \cup B) = \operatorname{cl}(A) \cup \operatorname{cl}(B) \text{ for any subsets }A,B \subseteq X$ (Preservation of Binary Union)
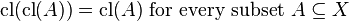$\operatorname{cl}(\operatorname{cl}(A)) = \operatorname{cl}(A) \text{ for every subset }A \subseteq X$ (Idempotence)

If the last axiom, idempotence, is omitted, then the axioms define a preclosure operator.

A consequence of the third axiom is: 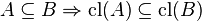$A \subseteq B \Rightarrow \operatorname{cl}(A) \subseteq \operatorname{cl}(B)$ (Preservation of Inclusion).^[3]

The four Kuratowski closure axioms can be replaced by a single condition, namely,^[4]

A \cup \operatorname{cl}(A) \cup \operatorname{cl}(\operatorname{cl}(B)) = \operatorname{cl}(A \cup B) \setminus \operatorname{cl}(\varnothing) \text{ for all subsets }A, B \subseteq X.

Connection to other axiomatizations of topology

Induction of Topology

Construction
A closure operator naturally induces a topology as follows:
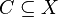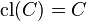A subset $C\subseteq X$ is called closed if and only if $\operatorname{cl}(C) = C$ .

Empty Set and Entire Space are closed:
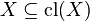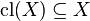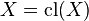By extensitivity, $X\subseteq\operatorname{cl}(X)$ and since closure maps the power set of $X$ into itself (that is, the image of any subset is a subset of $X$ ), $\operatorname{cl}(X)\subseteq X$ we have $X = \operatorname{cl}(X)$ . Thus $X$ is closed.
The preservation of nullary unions states that 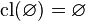$\operatorname{cl}(\varnothing) = \varnothing$ . Thus 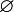$\varnothing$ is closed.

Arbitrary intersections of closed sets are closed:
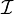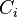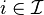Let $\mathcal{I}$ be an arbitrary set of indices and $C_i$ closed for every $i\in\mathcal{I}$ .
By extensitivity, 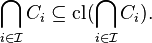$\bigcap_{i\in\mathcal{I}}C_i \subseteq \operatorname{cl}(\bigcap_{i\in\mathcal{I}}C_i).$
Also, by preservation of inclusions, 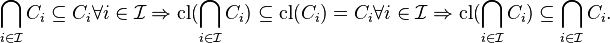$\bigcap_{i\in\mathcal{I}}C_i \subseteq C_i \forall i\in\mathcal{I} \Rightarrow \operatorname{cl}(\bigcap_{i\in\mathcal{I}}C_i) \subseteq \operatorname{cl}(C_i) = C_i \forall i\in\mathcal{I} \Rightarrow \operatorname{cl}(\bigcap_{i\in\mathcal{I}}C_i) \subseteq \bigcap_{i\in\mathcal{I}}C_i.$
Therefore, 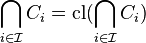$\bigcap_{i\in\mathcal{I}}C_i = \operatorname{cl}(\bigcap_{i\in\mathcal{I}}C_i)$ . Thus 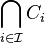$\bigcap_{i\in\mathcal{I}}C_i$ is closed.

Finite unions of closed sets are closed:
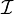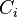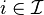Let $\mathcal{I}$ be a finite set of indices and let $C_i$ be closed for every $i\in\mathcal{I}$ .
From the preservation of binary unions and using induction we have 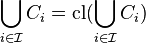$\bigcup_{i\in\mathcal{I}}C_i = \operatorname{cl}(\bigcup_{i\in\mathcal{I}}C_i)$ . Thus 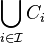$\bigcup_{i\in\mathcal{I}}C_i$ is closed.

Induction of closure

In any induced topology (relative to the subset A) the closed sets induce a new closure operator that is just the original closure operator restricted to A: 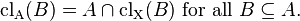$\operatorname{cl_A}(B) = A \cap \operatorname{cl_X}(B) \text{ for all } B \subseteq A.$ ^[5]

Recovering notions from topology

Closeness
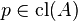A point $p$ is close to a subset $A$ iff $p\in\operatorname{cl}(A)$ .

Continuity
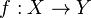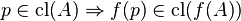A function $f:X\to Y$ is continuous at a point $p$ iff $p\in\operatorname{cl}(A) \Rightarrow f(p)\in\operatorname{cl}(f(A))$ .

Notes

↑ Kuratowski 1966, p. 38
↑ Kuratowski (1966) has a fifth (optional) axiom stating that singleton sets are their own closures. He refers to topological spaces which satisfy all five axioms as T₁ spaces in contrast to the more general spaces which only satisfy the four listed axioms.
↑ Pervin 1964, p. 43
↑ Pervin 1964, p. 42
↑ Pervin 1964, p. 49, Theorem 3.4.3

References

Kuratowski, K. (1966) [1958], Topology Volume I, Academic Press, ISBN 0-12-429201-1

Pervin, William J. (1964), Foundations of General Topology, Academic Press

External links

Alternative Characterizations of Topological Spaces