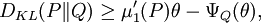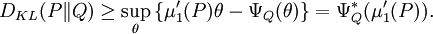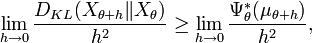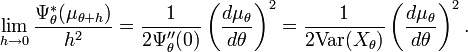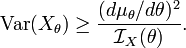Kullback's inequality
In information theory and statistics, Kullback's inequality is a lower bound on the Kullback–Leibler divergence expressed in terms of the large deviations rate function.[1] If P and Q are probability distributions on the real line, such that P is absolutely continuous with respect to Q, i.e. P<<Q, and whose first moments exist, then
where 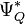 is the rate function, i.e. the convex conjugate of the cumulant-generating function, of
is the rate function, i.e. the convex conjugate of the cumulant-generating function, of 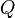 , and
, and  is the first moment of
is the first moment of 
The Cramér–Rao bound is a corollary of this result.
Proof
Let P and Q be probability distributions (measures) on the real line, whose first moments exist, and such that P<<Q. Consider the natural exponential family of Q given by
for every measurable set A, where 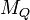 is the moment-generating function of Q. (Note that Q0=Q.) Then
is the moment-generating function of Q. (Note that Q0=Q.) Then
By Gibbs' inequality we have 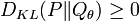 so that
so that
Simplifying the right side, we have, for every real θ where 
where  is the first moment, or mean, of P, and
is the first moment, or mean, of P, and  is called the cumulant-generating function. Taking the supremum completes the process of convex conjugation and yields the rate function:
is called the cumulant-generating function. Taking the supremum completes the process of convex conjugation and yields the rate function:
Corollary: the Cramér–Rao bound
Start with Kullback's inequality
Let Xθ be a family of probability distributions on the real line indexed by the real parameter θ, and satisfying certain regularity conditions. Then
where 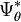 is the convex conjugate of the cumulant-generating function of
is the convex conjugate of the cumulant-generating function of 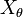 and
and 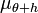 is the first moment of
is the first moment of 
Left side
The left side of this inequality can be simplified as follows:
![= \lim_{h\rightarrow 0} \frac 1 {h^2} \int_{-\infty}^\infty \left[
\left( 1 - \frac{\mathrm dX_\theta}{\mathrm dX_{\theta+h}} \right)
+\frac 1 2 \left( 1 - \frac{\mathrm dX_\theta}{\mathrm dX_{\theta+h}} \right) ^ 2
+ o \left( \left( 1 - \frac{\mathrm dX_\theta}{\mathrm dX_{\theta+h}} \right) ^ 2 \right)
\right]\mathrm dX_{\theta+h},](../I/m/11001159b5145e38a4b64bd0bfb8c09f.png)
- where we have expanded the logarithm
 in a Taylor series in
in a Taylor series in 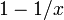 ,
,
- where we have expanded the logarithm
![= \lim_{h\rightarrow 0} \frac 1 {h^2} \int_{-\infty}^\infty \left[
\frac 1 2 \left( 1 - \frac{\mathrm dX_\theta}{\mathrm dX_{\theta+h}} \right) ^ 2
\right]\mathrm dX_{\theta+h}](../I/m/38e488d4485a2810c4b189ff37433b46.png)
![= \lim_{h\rightarrow 0} \frac 1 {h^2} \int_{-\infty}^\infty \left[
\frac 1 2 \left( \frac{\mathrm dX_{\theta+h} - \mathrm dX_\theta}{\mathrm dX_{\theta+h}} \right) ^ 2
\right]\mathrm dX_{\theta+h}
= \frac 1 2 \mathcal I_X(\theta),](../I/m/04a0aa04fe99cd2d5eaceb80c404a804.png)
which is half the Fisher information of the parameter θ.
Right side
The right side of the inequality can be developed as follows:
This supremum is attained at a value of t=τ where the first derivative of the cumulant-generating function is  but we have
but we have 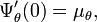 so that
so that
Moreover,
Putting both sides back together
We have:
which can be rearranged as:
See also
- Kullback–Leibler divergence
- Cramér–Rao bound
- Fisher information
- Large deviations theory
- Convex conjugate
- Rate function
- Moment-generating function
Notes and references
- ↑ Fuchs, Aimé; Letta, Giorgio (1970). L'inégalité de Kullback. Application à la théorie de l'estimation. Séminaire de probabilités 4. Strasbourg. pp. 108–131.