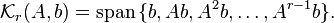Krylov subspace

In linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r-1 powers of A (starting from 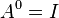A^0=I), that is,

\mathcal{K}_r(A,b) = \operatorname{span} \, \{ b, Ab, A^2b, \ldots, A^{r-1}b \}. \,

Background

It is named after Russian applied mathematician and naval engineer Alexei Krylov, who published a paper about it in 1931. The basis for the Krylov subspace is derived from the Cayley–Hamilton theorem which says that the inverse of a matrix can be found in terms of a linear combination of its powers.[1][2]

Use

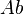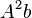Modern iterative methods for finding one (or a few) eigenvalues of large sparse matrices or solving large systems of linear equations avoid matrix-matrix operations, but rather multiply vectors by the matrix and work with the resulting vectors. Starting with a vector, b, one computes A b, then one multiplies that vector by A to find A^2 b and so on. All algorithms that work this way are referred to as Krylov subspace methods; they are among the most successful methods currently available in numerical linear algebra.

Issues

Because the vectors usually soon become almost linearly dependent due to the properties of power iteration, methods relying on Krylov subspace frequently involve some orthogonalization scheme, such as Lanczos iteration for Hermitian matrices or Arnoldi iteration for more general matrices.

Existing methods

The best known Krylov subspace methods are the Arnoldi, Lanczos, Conjugate gradient, IDR(s) (Induced dimension reduction), GMRES (generalized minimum residual), BiCGSTAB (biconjugate gradient stabilized), QMR (quasi minimal residual), TFQMR (transpose-free QMR), and MINRES (minimal residual) methods.

References

  1. ↑ Mike Botchev (2002). "A.N.Krylov, a short biography".6 Dec. 2012.
  2. ↑ Grigorian, A. T. (2008). "Krylov, Aleksei Nikolaevich." Complete Dictionary of Scientific Biography. 2008. Encyclopedia.com. 6 Dec. 2012.

Bibliography