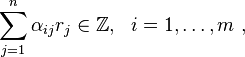Kronecker's theorem

For the theorem about the real analytic Eisenstein series see Kronecker limit formula.

In mathematics, Kronecker's theorem is either of two theorems named after Leopold Kronecker.

The existence of extension fields

This is a theorem stating that a non-constant polynomial in a field, p(x) ∈ F[x], has a root in an extension field 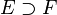E \supset F.[1]

For example, a polynomial in the reals such as x2 + 1 = 0 has two roots, both in the complex field.

This theorem is usually credited to Kronecker despite his original reluctance to accept the existence of numbers outside of the rationals;[2] it provides a useful construction of many sets.

A result in diophantine approximation

Kronecker's theorem may also refer to a result in diophantine approximations applying to several real numbers xi, for 1 ≤ i ≤ n, that generalises Dirichlet's approximation theorem to multiple variables.

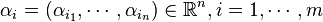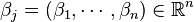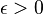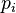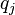The classical Kronecker's approximation theorem is formulated as follows; Given real numbers \alpha_i=(\alpha_{i_1},\cdots,\alpha_{i_n})\in\mathbb{R}^n, i=1,\cdots,m and \beta_j=(\beta_1,\cdots,\beta_n)\in \mathbb{R}^n , for any small \epsilon>0 there exist integers p_i and q_j such that

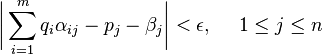\biggl| \sum^m_{i=1}q_i\alpha_{ij}-p_j-\beta_j\biggr|<\epsilon,\ \ \ \ 1\le j\le n ,

if and only if for any 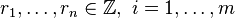r_1,\dots,r_n\in\mathbb{Z},\ i=1,\dots,m with

\sum^n_{j=1}\alpha_{ij}r_j\in\mathbb{Z}, \ \ i=1,\dots,m\ ,

the number 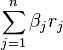\sum^n_{j=1}\beta_jr_j is also an integer.

Kronecker's approximation theorem had been firstly proved by L. Kronecker in the end of the 19-th century. It has been now revealed to relate to the idea of n-torus and Mahler measure since the later half of the 20-th century. In terms of physical systems, it has the consequence that planets in circular orbits moving uniformly around a star will, over time, assume all alignments, unless there is an exact dependency between their orbital periods.

the relation to n-torus

In the case of N numbers, taken as a single N-tuple and point P of the torus

T = RN/ZN,

the closure of the subgroup <P> generated by P will be finite, or some torus T′ contained in T. The original Kronecker's theorem (Leopold Kronecker, 1884) stated that the necessary condition for

T′ = T,

which is that the numbers xi together with 1 should be linearly independent over the rational numbers, is also sufficient. Here it is easy to see that if some linear combination of the xi and 1 with non-zero rational number coefficients is zero, then the coefficients may be taken as integers, and a character χ of the group T other than the trivial character takes the value 1 on P. By Pontryagin duality we have T′ contained in the kernel of χ, and therefore not equal to T.

In fact a thorough use of Pontryagin duality here shows that the whole Kronecker theorem describes the closure of <P> as the intersection of the kernels of the χ with

χ(P) = 1.

This gives an (antitone) Galois connection between monogenic closed subgroups of T (those with a single generator, in the topological sense), and sets of characters with kernel containing a given point. Not all closed subgroups occur as monogenic; for example a subgroup that has a torus of dimension ≥ 1 as connected component of the identity element, and that is not connected, cannot be such a subgroup.

The theorem leaves open the question of how well (uniformly) the multiples mP of P fill up the closure. In the one-dimensional case, the distribution is uniform by the equidistribution theorem.

See also

Notes and references

Hazewinkel, Michiel, ed. (2001), "Kronecker's theorem", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

  1. ↑ Applied Abstract Algebra by D. Joyner, R. Kreminski and J. Turisco.
  2. ↑ Allenby, R. B. J. T. (1983). Rings, fields and groups: an introduction to abstract algebra. London: E. Arnold. pp. 140,141. ISBN 0-7131-3476-3.