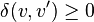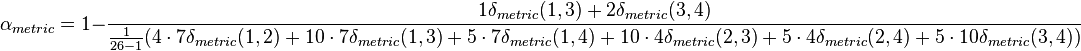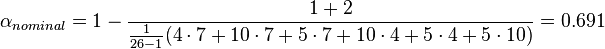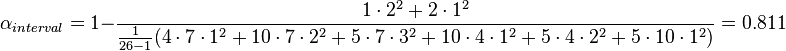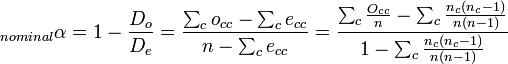Krippendorff's alpha
Krippendorff's alpha coefficient[1] is a statistical measure of the agreement achieved when coding a set of units of analysis in terms of the values of a variable. Since the 1970s, alpha is used in content analysis where textual units are categorized by trained readers, in counseling and survey research where experts code open-ended interview data into analyzable terms, in psychological testing where alternative tests of the same phenomena need to be compared, or in observational studies where unstructured happenings are recorded for subsequent analysis.
Krippendorff’s alpha generalizes several known statistics, often called measures of inter-coder agreement, inter-rater reliability, reliability of coding given sets of units (as distinct from unitizing) but it also distinguishes itself from statistics that are called reliability coefficients but are unsuitable to the particulars of coding data generated for subsequent analysis.
Krippendorff’s alpha is applicable to any number of coders, each assigning one value to one unit of analysis, to incomplete (missing) data, to any number of values available for coding a variable, to binary, nominal, ordinal, interval, ratio, polar, and circular metrics (Levels of Measurement), and it adjusts itself to small sample sizes of the reliability data. The virtue of a single coefficient with these variations is that computed reliabilities are comparable across any numbers of coders, values, different metrics, and unequal sample sizes.
Software for calculating Krippendorff’s alpha is available.[2][3][4][5]
Reliability data
Reliability data are generated in a situation in which m ≥ 2 jointly instructed (e.g., by a Code book) but independently working coders assign any one of a set of values 1,...,V to a common set of N units of analysis. In their canonical form, reliability data are tabulated in an m-by-N matrix containing n values vij that coder ci has assigned to unit uj. Define mj as the number of values assigned to unit j across all coders c. When data are incomplete, mj may be less than m. Reliability data require that values be pairable, i.e., mj ≥ 2. The total number of pairable values is n ≤ mN.
To help clarify, here is what the canonical form looks like, in the abstract:
| u1 | u2 | u3 | ... | uN | |
|---|---|---|---|---|---|
| c1 | v11 | v12 | v13 | ... | v1N |
| c2 | v21 | v22 | v23 | ... | v2N |
| c3 | v31 | v32 | v33 | ... | v3N |
| ... | ... | ... | ... | ... | ... |
| cm | vm1 | vm2 | vm3 | ... | vmN |
General form of alpha
where the disagreement
is the average difference 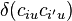 between two values ciu and ci'u over all mu(mu-1) pairs of values possible within unit u – without reference to coders.
between two values ciu and ci'u over all mu(mu-1) pairs of values possible within unit u – without reference to coders. 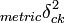 is a function of the metric of the variable, see below. The observed disagreement
is a function of the metric of the variable, see below. The observed disagreement
is the average over all unit-wise disagreements in the data. And the expected disagreement
is the average difference between any two values ciu and ci'u' over all n(n–1) pairs of values possible within the reliability data – without reference to coders or units. In effect, De is the disagreement that is expected when the values used by all coders are randomly assigned to the given set of units.
One interpretation of Krippendorff's alpha is: 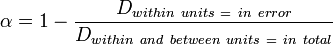
- α = 1 indicates perfect reliability
- α = 0 indicates the absence of reliability. Units and the values assigned to them are statistically unrelated
- α < 0 when disagreements are systematic and exceed what can be expected by chance.
- α = 1 indicates perfect reliability
In this general form, disagreements Do and De may be conceptually transparent but are computationally inefficient. They can be simplified algebraically, especially when expressed in terms of the visually more instructive coincidence matrix representation of the reliability data.
Coincidence matrices
A coincidence matrix cross tabulates the n pairable values from the canonical form of the reliability data into a v-by-v square matrix, where v is the number of values available in a variable. Unlike contingency matrices, familiar in association and correlation statistics, which tabulate pairs of values (Cross tabulation), a coincidence matrix tabulates all pairable values. A coincidence matrix omits references to coders and is symmetrical around its diagonal, which contains all perfect matches, viu = vi'u for two coders i and i' , across all units u. The matrix of observed coincidences contains frequencies:
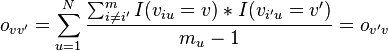 ,
,
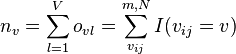 ,
, 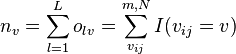 , and
, and 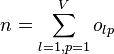 ,
,
omitting unpaired values, where I(∘) = 1 if ∘ is true, and 0 otherwise.
Because a coincidence matrix tabulates all pairable values and its contents sum to the total n, when four or more coders are involved, ock may be fractions.
The matrix of expected coincidences contains frequencies:
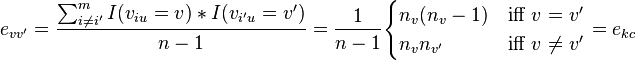 ,
,
which sum to the same nc, nk, and n as does ock. In terms of these coincidences, Krippendorff's alpha becomes:
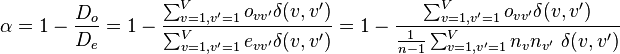 .
.
Difference functions
Difference functions 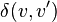 [6] between values v and v' reflect the metric properties (Levels of Measurement) of their variable.
[6] between values v and v' reflect the metric properties (Levels of Measurement) of their variable.
In general:
In particular:
- For nominal data
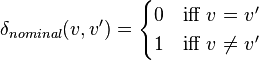 , where v and v' serve as names.
, where v and v' serve as names. - For ordinal data
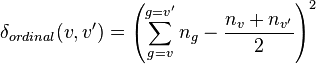 , where v and v' are ranks.
, where v and v' are ranks.
- For nominal data
- For interval data
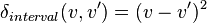 , where v and v' are interval scale values.
, where v and v' are interval scale values.
- For interval data
- For ratio data
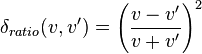 , where v and v' are absolute values.
, where v and v' are absolute values. - For polar data
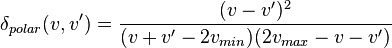 , where vmin and vmax define the end points of the polar scale.
, where vmin and vmax define the end points of the polar scale. - For circular data
![\delta_{circular}(v,v') = \left ( \sin \left [180 \frac{v-v'}{U} \right ] \right )^2](../I/m/7232fe14387fa9239325c95106714a15.png) , where the sine function is expressed in degrees and U is the circumference or the range of values in a circle or loop before they repeat. For equal interval circular metrics, the smallest and largest integer values of this metric are adjacent to each other and U = vlargest – vsmallest + 1.
, where the sine function is expressed in degrees and U is the circumference or the range of values in a circle or loop before they repeat. For equal interval circular metrics, the smallest and largest integer values of this metric are adjacent to each other and U = vlargest – vsmallest + 1.
- For ratio data
Significance
Inasmuch as mathematical statements of the statistical distribution of alpha are always only approximations, it is preferable to obtain alpha’s distribution by bootstrapping.[7][8] Alpha 's distribution gives rise to two indices:
- The confidence intervals of a computed alpha at various levels of statistical significance
- The probability that alpha fails to achieve a chosen minimum, required for data to be considered sufficiently reliable (one-tailed test). This index acknowledges that the null-hypothesis (of chance agreement) is so far removed from the range of relevant alpha coefficients that its rejection would mean little regarding how reliable given data are. To be judged reliable, data must not significantly deviate from perfect agreement.
The minimum acceptable alpha coefficient should be chosen according to the importance of the conclusions to be drawn from imperfect data. When the costs of mistaken conclusions are high, the minimum alpha needs to be set high as well. In the absence of knowledge of the risks of drawing false conclusions from unreliable data, social scientists commonly rely on data with reliabilities α ≥ .800, consider data with 0.800 > α ≥ 0.667 only to draw tentative conclusions, and discard data whose agreement measures α < 0.667.[9]
A misunderstanding of Krippendorff's alpha has become an instructive public controversy.[10]
A computational example
Let the canonical form of reliability data be a 3-coder-by-15 unit matrix with 45 cells:
| Units u: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coder A | * | * | * | * | * | 3 | 4 | 1 | 2 | 1 | 1 | 3 | 3 | * | 3 |
| Coder B | 1 | * | 2 | 1 | 3 | 3 | 4 | 3 | * | * | * | * | * | * | * |
| Coder C | * | * | 2 | 1 | 3 | 4 | 4 | * | 2 | 1 | 1 | 3 | 3 | * | 4 |
Suppose “*” indicates a default category like “cannot code,” “no answer,” or “lacking an observation.” Then, * provides no information about the reliability of data in the four values that matter. Note that unit 2 and 14 contains no information and unit 1 contains only one value, which is not pairable within that unit. Thus, these reliability data consist not of mN=45 but of n=36 pairable values, not in N =15 but in 12 multiply coded units.
The coincidence matrix for these data would be constructed as follows:
- o11 = {in u=4}:
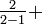 {in u=10}:
{in u=10}: 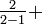 {in u=11};
{in u=11}; 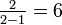
- o11 = {in u=4}:
- o13 = {in u=8}:
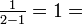 o31
o31
- o13 = {in u=8}:
- o22 = {in u=3}:
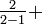 {in u=9}:
{in u=9}: 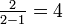
- o22 = {in u=3}:
- o33 = {in u=5}:
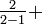 {in u=6}:
{in u=6}: 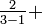 {in u=12}:
{in u=12}: 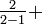 {in u=13}:
{in u=13}: 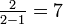
- o33 = {in u=5}:
- o34 = {in u=6}:
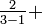 {in u=15}:
{in u=15}: 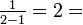 o43
o43
- o34 = {in u=6}:
- o44 = {in u=7}:
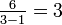
- o44 = {in u=7}:
| Values v or v' : | 1 | 2 | 3 | 4 | nv |
|---|---|---|---|---|---|
| Value 1 | 6 | 1 | 7 | ||
| Value 2 | 4 | 4 | |||
| Value 3 | 1 | 7 | 2 | 10 | |
| Value 4 | 2 | 3 | 5 | ||
| Frequency nv' | 7 | 4 | 10 | 5 | 26 |
In terms of the entries in this coincidence matrix, Krippendorff's alpha may be calculated from:
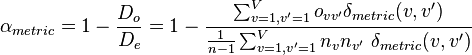 .
.
For convenience, because products with 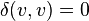 and
and 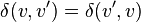 , only the entries in one of the off-diagonal triangles of the coincidence matrix are listed in the following:
, only the entries in one of the off-diagonal triangles of the coincidence matrix are listed in the following:
Considering that all 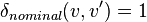 when
when 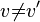 for nominal data the above expression yields:
for nominal data the above expression yields:
With 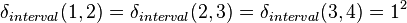 ,
, 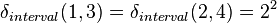 , and
, and 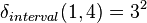 , for interval data the above expression yields:
, for interval data the above expression yields:
Here, 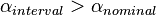 because disagreements happens to occur largely among neighboring values, visualized by occurring closer to the diagonal of the coincidence matrix, a condition that
because disagreements happens to occur largely among neighboring values, visualized by occurring closer to the diagonal of the coincidence matrix, a condition that 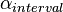 takes into account but
takes into account but 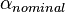 does not. When the observed frequencies ov≠ v' are on the average proportional to the expected frequencies ev ≠ v',
does not. When the observed frequencies ov≠ v' are on the average proportional to the expected frequencies ev ≠ v', 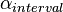 =
= 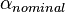 .
.
Comparing alpha coefficients across different metrics can provide clues to how coders conceptualize the metric of a variable.
Alpha's embrace of other statistics
Krippendorff's alpha brings several known statistics under a common umbrella, each of them has its own limitations but no additional virtues.
- Scott’s pi[11] is an agreement coefficient for nominal data and two coders.
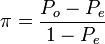 where
where 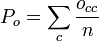 , and
, and 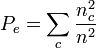
- When data are nominal, alpha reduces to a form resembling Scott’s pi:
- Scott’s observed proportion of agreement
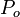 appears in alpha’s numerator, exactly. Scott’s expected proportion of agreement,
appears in alpha’s numerator, exactly. Scott’s expected proportion of agreement, 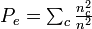 is asymptotically approximated by
is asymptotically approximated by 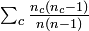 when the sample size n is large, equal when infinite. It follows that Scott’s pi is that special case of alpha in which two coders generate a very large sample of nominal data. For finite sample sizes:
when the sample size n is large, equal when infinite. It follows that Scott’s pi is that special case of alpha in which two coders generate a very large sample of nominal data. For finite sample sizes: 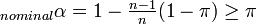 . Evidently,
. Evidently, 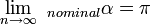 .
.
- Fleiss’ kappa[12] is an agreement coefficient for nominal data, a fixed number of m coders, each coding all of N units without exception, and very large sample sizes. Fleiss claimed to have extended Cohen’s kappa[13] to three or more raters or coders, but generalized Scott’s pi instead. This confusion is reflected in Fleiss’ choice of its name, which has been recognized by renaming it K:[14]
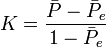 where
where 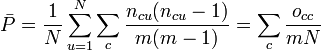 , and
, and 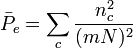
- When sample sizes are finite, K can be seen to perpetrate the inconsistency of obtaining the proportion of observed agreements
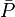 by counting matches within the m(m-1) possible pairs of values within u, properly excluding values paired with themselves, while the proportion
by counting matches within the m(m-1) possible pairs of values within u, properly excluding values paired with themselves, while the proportion 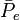 is obtained by counting matches within all (mN)2=n2 possible pairs of values, effectively including values paired with themselves. It is the latter that introduces a bias into the coefficient. However, just as for pi, when sample sizes become very large this bias disappears and the proportion
is obtained by counting matches within all (mN)2=n2 possible pairs of values, effectively including values paired with themselves. It is the latter that introduces a bias into the coefficient. However, just as for pi, when sample sizes become very large this bias disappears and the proportion 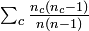 in nominalα above asymptotically approximates
in nominalα above asymptotically approximates 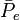 in K. Nevertheless, Fleiss' kappa, or rather K, intersects with alpha in that special situation in which a fixed number of m coders code all of N units (no data are missing), using nominal categories, and the sample size n=mN is very large, theoretically infinite.
in K. Nevertheless, Fleiss' kappa, or rather K, intersects with alpha in that special situation in which a fixed number of m coders code all of N units (no data are missing), using nominal categories, and the sample size n=mN is very large, theoretically infinite.
- Spearman’s rank correlation coefficient rho[15] measures the agreement between two coders’ ranking of the same set of N objects. In its original form:
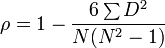 ,
,
- where
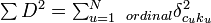 is the sum of N differences between one coder’s rank c and the other coder’s rank k of the same object u. Whereas alpha accounts for tied ranks in terms of their frequencies for all coders, rho averages them in each individual coder's instance. In the absence of ties,
is the sum of N differences between one coder’s rank c and the other coder’s rank k of the same object u. Whereas alpha accounts for tied ranks in terms of their frequencies for all coders, rho averages them in each individual coder's instance. In the absence of ties,  's numerator
's numerator 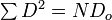 and
and  's denominator
's denominator 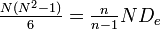 , where n=2N, which becomes
, where n=2N, which becomes 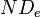 when sample sizes become large. So, Spearman’s rho is that special case of alpha in which two coders rank a very large set of units. Again,
when sample sizes become large. So, Spearman’s rho is that special case of alpha in which two coders rank a very large set of units. Again, 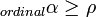 and
and 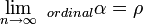 .
.
- Pearson’s intraclass correlation coefficient rii is an agreement coefficient for interval data, two coders, and very large sample sizes. To obtain it, Pearson's original suggestion was to enter the observed pairs of values twice into a table, once as c-k and once as k-c, to which the traditional Pearson product-moment correlation coefficient is then applied.[16] By entering pairs of values twice, the resulting table becomes a coincidence matrix without reference to the two coders, contains n=2N values, and is symmetrical around the diagonal, i.e., the joint linear regression line is forced into a 45° line, and references to coders are eliminated. Hence, Pearson’s intraclass correlation coefficient is that special case of interval alpha for two coders and large sample sizes,
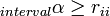 and
and  .
.
- Finally, The disagreements in the interval alpha, Du, Do and De are proper sample variances.[17] It follows that the reliability the interval alpha assesses is consistent with all variance-based analytical techniques, such as the Analysis of Variance. Moreover, by incorporating difference functions not just for interval data but also for nominal, ordinal, ratio, polar, and circular data, alpha extends the notion of variance to metrics that classical analytical techniques rarely address.
Krippendorff's alpha is more general than any of these special purpose coefficients. It adjusts to varying sample sizes and affords comparisons across a wide variety of reliability data, mostly ignored by the familiar measures.
Coefficients incompatible with alpha and the reliability of coding
Semantically, reliability is the ability to rely on something, here on coded data for subsequent analysis. When a sufficiently large number of coders agree perfectly on what they have read or observed, relying on their descriptions is a safe bet. Judgments of this kind hinge on the number of coders duplicating the process and how representative the coded units are of the population of interest. Problems of interpretation arise when agreement is less than perfect, especially when reliability is absent.
- Correlation and association coefficients. Pearson’s product-moment correlation coefficient rij, for example, measures deviations from any linear regression line between the coordinates of i and j. Unless that regression line happens to be exactly 45° or centered, rij does not measure agreement. Similarly, while perfect agreement between coders also means perfect association, association statistics register any above chance pattern of relationships between variables. They do not distinguish agreement from other associations and are, hence, unsuitable as reliability measures.
- Coefficients measuring the degree to which coders are statistically dependent on each other. When the reliability of coded data is at issue, the individuality of coders can have no place in it. Coders need to be treated as interchangeable. Alpha, Scott’s pi, and Pearson’s original intraclass correlation accomplish this by being definable as a function of coincidences, not only of contingencies. Unlike the more familiar contingency matrices, which tabulate N pairs of values and maintain reference to the two coders, coincidence matrices tabulate the n pairable values used in coding, regardless of who contributed them, in effect treating coders as interchangeable. Cohen’s kappa,[18] by contrast, defines expected agreement in terms of contingencies, as the agreement that would be expected if coders were statistically independent of each other.[19] Cohen's conception of chance fails to include disagreements between coders’ individual predilections for particular categories, punishes coders who agree on their use of categories, and rewards those who do not agree with higher kappa-values. This is the cause of other noted oddities of kappa.[20] The statistical independence of coders is only marginally related to the statistical independence of the units coded and the values assigned to them. Cohen’s kappa, by ignoring crucial disagreements, can become deceptively large when the reliability of coding data is to be assessed.
- Coefficients measuring the consistency of coder judgments. In the psychometric literature,[21] reliability tends to be defined as the consistency with which several tests perform when applied to a common set of individual characteristics. Cronbach’s alpha,[22] for example, is designed to assess the degree to which multiple tests produce correlated results. Perfect agreement is the ideal, of course, but Cronbach’s alpha is high also when test results vary systematically. Consistency of coders’ judgments does not provide the needed assurances of data reliability. Any deviation from identical judgments – systematic or random – needs to count as disagreement and reduce the measured reliability. Cronbach’s alpha is not designed to respond to absolute differences.
- Coefficients with baselines (conditions under which they measure 0) that cannot be interpreted in terms of reliability, i.e. have no dedicated value to indicate when the units and the values assigned to them are statistically unrelated. Simple %-agreement ranges from 0=extreme disagreement to 100=perfect agreement with chance having no definite value. As already noted, Cohen's kappa falls into this category by defining the absence of reliability as the statistical independence between two individual coders. The baseline of Bennett, Alpert, and Goldstein’s S[23] is defined in terms of the number of values available for coding, which has little to do with how values are actually used. Goodman and Kruskal’s lambdar[24] is defined to vary between –1 and +1, leaving 0 without a particular reliability interpretation. Lin’s reproducibility or concordance coefficient rc[25] takes Pearson’s product moment correlation rij as a measure of precision and adds to it a measure Cb of accuracy, ostensively to correct for rij's above mentioned inadequacy. It varies between –1 and +1 and the reliability interpretation of 0 is uncertain. There are more so-called reliability measures whose reliability interpretations become questionable as soon as they deviate from perfect agreement.
Naming a statistic as one of agreement, reproducibility, or reliability does not make it a valid index of whether one can rely on coded data in subsequent decisions. Its mathematical structure must fit the process of coding units into a system of analyzable terms.
Notes
- ↑ Krippendorff, K. (2013) pp. 221-250 describes the mathematics of alpha and its use in content analysis since 1969.
- ↑ Hayes, A. F. & Krippendorff, K. (2007) describe and provide SPSS and SAS macros for computing alpha, its confidence limits and the probability of failing to reach a chosen minimum.
- ↑ Manual page of the kripp.alpha() function for the platform independent statistics package R
- ↑ The Alpha resources page.
- ↑ Matlab code to compute Krippendorff's alpha.
- ↑ Computing Krippendorff’s Alpha Reliability” http://repository.upenn.edu/asc_papers/43/
- ↑ Krippendorff, K. (2004) pp. 237-238
- ↑ Hayes, A. F. & Krippendorff, K. (2007)
- ↑ Krippendorff, K. (2004) pp. 241-243
- ↑ Brooks, R. “Sweet Jesus I love Bill Reilly!” Los Angeles Times, May 4, 2007, http://www.latimes.com/news/opinion/commentary/la-oe-brooks4may04,0,6548272.column?coll=la-home-commentary; Mitchell, R. “Stop calling O’Reilly names.” Los Angeles Times, May 10, 2007, http://www.latimes.com/news/opinion/la-oew-mitchell9may09,0,3143633.story?coll=la-opinion-center; Conway, M., Grabe, M. E., & Grieves, K. "Bill O'Reilly and Krippendorff's Alpha." Los Angeles Times May 16, 2007, http://www.latimes.com/news/opinion/la-oew-conway16may16,0,3767872.story?coll=la-opinion-center; Convey, M., et al. “Peas in a pod; LA Times op-ed.
- ↑ Scott, W. A. (1955)
- ↑ Fleiss, J. L. (1971)
- ↑ Cohen, J. (1960)
- ↑ Siegel, S. & Castellan, N. J. (1988), pp. 284-291.
- ↑ Spearman, C. E. (1904)
- ↑ Pearson, K. (1901), Tildesley, M. L. (1921)
- ↑ Krippendorff, K. (1970)
- ↑ Cohen, J. (1960)
- ↑ Krippendorff, K. (1978) raised this issue with Joseph Fleiss
- ↑ Zwick, R. (1988), Brennan, R. L. & Prediger, D. J. (1981), Krippendorff (1978, 2004).
- ↑ Nunnally, J. C. & Bernstein, I. H. (1994)
- ↑ Cronbach, L. J. (1951)
- ↑ Bennett, E. M., Alpert, R. & Goldstein, A. C. (1954)
- ↑ Goodman, L. A. & Kruskal, W. H. (1954) p. 758
- ↑ Lin, L. I. (1989)
References
- Bennett, Edward M., Alpert, R. & Goldstein, A. C. (1954). Communications through limited response questioning. Public Opinion Quarterly, 18, 303-308.
- Brennan, Robert L. & Prediger, Dale J. (1981). Coefficient kappa: Some uses, misuses, and alternatives. Educational and Psychological Measurement, 41, 687-699.
- Cohen, Jacob (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20 (1), 37-46.
- Cronbach, Lee, J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16 (3), 297-334.
- Fleiss, Joseph L. (1971). Measuring nominal scale agreement among many raters. Psychological Bulletin, 76, 378-382.
- Goodman, Leo A. & Kruskal, William H. (1954). Measures of association for cross classifications. Journal of the American Statistical Association, 49, 732-764.
- Hayes, Andrew F. & Krippendorff, Klaus (2007). Answering the call for a standard reliability measure for coding data. Communication Methods and Measures, 1, 77-89.
- Krippendorff, Klaus (2013). Content analysis: An introduction to its methodology, 3rd edition. Thousand Oaks, CA: Sage.
- Krippendorff, Klaus (1978). Reliability of binary attribute data. Biometrics, 34 (1), 142-144.
- Krippendorff, Klaus (1970). Estimating the reliability, systematic error, and random error of interval data. Educational and Psychological Measurement, 30 (1),61-70.
- Lin, Lawrence I. (1989). A concordance correlation coefficient to evaluate reproducibility. Biometrics, 45, 255-268.
- Nunnally, Jum C. & Bernstein, Ira H. (1994). Psychometric Theory, 3rd ed. New York: McGraw-Hill.
- Pearson, Karl, et al. (1901). Mathematical contributions to the theory of evolution. IX: On the principle of homotyposis and its relation to heredity, to variability of the individual, and to that of race. Part I: Homotyposis in the vegetable kingdom. Philosophical Transactions of the Royal Society (London), Series A, 197, 285-379.
- Scott, William A. (1955). Reliability of content analysis: The case of nominal scale coding. Public Opinion Quarterly, 19, 321-325.
- Siegel, Sydney & Castella, N. John (1988). Nonparametric Statistics for the Behavioral Sciences, 2nd ed. Boston: McGraw-Hill.
- Tildesley, M. L. (1921). A first study of the Burmes skull. Biometrica, 13, 176-267.
- Spearman, Charles E. (1904). The proof and measurement of association between two things. American Journal of Psychology, 15, 72–101.
- Zwick, Rebecca (1988). Another look at interrater agreement. Psychological Bulletin, 103 (3), 347-387.
External links
- Reliability Calculator calculates Krippendorff’s alpha.
- Online inter-rater agreement calculator includes Krippendorff’s alpha.
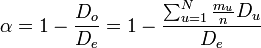
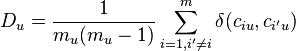
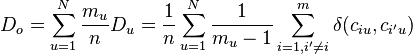
![D_e = \frac{1}{n(n-1)} \sum_{u=1,u'=1}^{N} \sum_{i=1,i'=1}^{m} \delta (c_{iu}, c_{i'u'}), [(i,u) \ne (i',u')]](../I/m/c06f815bfc78a63566a7694f76a13304.png)