Krener's theorem
In mathematics, Krener's theorem is a result attributed to Arthur J. Krener in geometric control theory about the topological properties of attainable sets of finite-dimensional control systems. It states that any attainable set of a bracket-generating system has nonempty interior or, equivalently, that any attainable set has nonempty interior in the topology of the corresponding orbit. Heuristically, Krener's theorem prohibits attainable sets from being hairy.
Theorem
Let
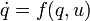 be a smooth control system, where
be a smooth control system, where
 belongs to a finite-dimensional manifold
belongs to a finite-dimensional manifold 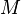 and
and 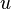 belongs to a control set
belongs to a control set 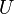 . Consider the family of vector fields
. Consider the family of vector fields  .
.
Let 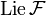 be the Lie algebra generated by
be the Lie algebra generated by  with respect to the Lie bracket of vector fields.
Given
with respect to the Lie bracket of vector fields.
Given 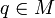 , if the vector space
, if the vector space 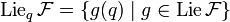 is equal to
is equal to  ,
then
,
then 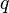 belongs to the closure of the interior of the attainable set from
belongs to the closure of the interior of the attainable set from 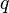 .
.
Remarks and consequences
Even if  is different from
is different from  ,
the attainable set from
,
the attainable set from 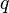 has nonempty interior in the orbit topology,
as it follows from Krener's theorem applied to the control system restricted to the orbit through
has nonempty interior in the orbit topology,
as it follows from Krener's theorem applied to the control system restricted to the orbit through 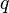 .
.
When all the vector fields in 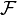 are analytic,
are analytic, 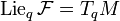 if and only if
if and only if 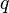 belongs to the closure of the interior of the attainable set from
belongs to the closure of the interior of the attainable set from 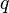 . This is a consequence of Krener's theorem and of the orbit theorem.
. This is a consequence of Krener's theorem and of the orbit theorem.
As a corollary of Krener's theorem one can prove that if the system is bracket-generating and if the attainable set from 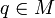 is dense in
is dense in 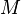 , then the attainable set from
, then the attainable set from 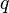 is actually equal to
is actually equal to 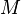 .
.
References
- Agrachev, Andrei A.; Sachkov, Yuri L. (2004). Control theory from the geometric viewpoint. Springer-Verlag. pp. xiv+412. ISBN 3-540-21019-9.
- Jurdjevic, Velimir (1997). Geometric control theory. Cambridge University Press. pp. xviii+492. ISBN 0-521-49502-4.
- Sussmann, Héctor J.; Jurdjevic, Velimir (1972). "Controllability of nonlinear systems". J. Differential Equations 12 (1): 95–116. doi:10.1016/0022-0396(72)90007-1.
- Krener, Arthur J. (1974). "A generalization of Chow's theorem and the bang-bang theorem to non-linear control problems". SIAM J. Control Optim. 12: 43–52.