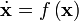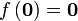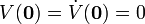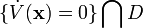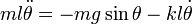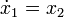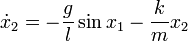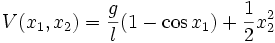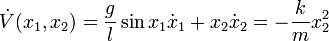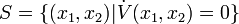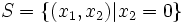Krasovskii–LaSalle principle

The Krasovskii–LaSalle principle (also known as the invariance principle^[1]) is a criterion for the asymptotic stability of an autonomous (possibly nonlinear) dynamical system.

The global Krasovskii–LaSalle principle

Given a representation of the system

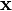\dot{\mathbf{x}} = f \left(\mathbf x \right)

where $\mathbf x$ is the vector of variables, with

f \left( \mathbf 0 \right) = \mathbf 0

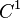If a $C^1$ function 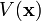$V(\mathbf x)$ can be found such that

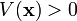V( \mathbf x) > 0

, for all

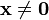\mathbf x \neq \mathbf 0

(positive definite)

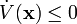\dot{V}(\mathbf x) \le 0

for all

\mathbf x

(negative semidefinite)

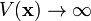V(\mathbf x) \to \infty

, if

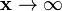
\mathbf x \to \infty

and

V( \mathbf 0) = \dot{V} (\mathbf 0) = 0

(Such functions can be thought of as "energy-like".)

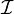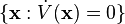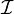Let ${\mathcal I}$ be the union of complete trajectories contained entirely in the set $\{\mathbf x : \dot{V}( \mathbf x) = 0 \}$ . Then the set of accumulation points of any trajectory is contained in ${\mathcal I}$ .

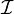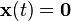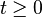In particular, if ${\mathcal I}$ contains no trajectory of the system except the trivial trajectory $\mathbf x(t) = \mathbf 0$ for $t \geq 0$ , then the origin is globally asymptotically stable.

Local version of the Krasovskii–LaSalle principle

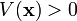V( \mathbf x) > 0

, when

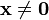
\mathbf x \neq \mathbf 0

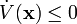
\dot{V}(\mathbf x) \le 0

hold only for 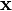$\mathbf x$ in some neighborhood 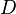$D$ of the origin, and the set

\{ \dot{V}( \mathbf x) = 0 \} \bigcap D

does not contain any trajectories of the system besides the trajectory 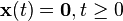$\mathbf x(t)=\mathbf 0, t \geq 0$ , then the local version of the Krasovskii–LaSalle principle states that the origin is locally asymptotically stable.

Relation to Lyapunov theory

If 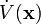$\dot{V} ( \mathbf x)$ is negative definite, the global asymptotic stability of the origin is a consequence of Lyapunov's second theorem. The Krasovskii–LaSalle principle gives a criterion for asymptotic stability in the case when 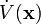$\dot{V} ( \mathbf x)$ is only negative semidefinite.

Example: the pendulum with friction

This section will apply the Krasovskii–LaSalle principle to establish the local asymptotic stability of a simple system, the pendulum with friction. This system can be modeled with the differential equation

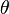m l \ddot{\theta} = - m g \sin \theta - k l \dot{\theta}

where $\theta$ is the angle the pendulum makes with the vertical normal, 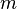$m$ is the mass of the pendulum, 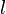$l$ is the length of the pendulum, 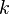$k$ is the friction coefficient, and g is acceleration due to gravity.

This, in turn, can be written as the system of equations

\dot{x}_1 = x_2

\dot{x}_2 = -\frac{g}{l} \sin x_1 - \frac{k}{m} x_2

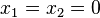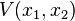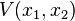Using the Krasovskii–LaSalle principle, it can be shown that all trajectories which begin in a ball of certain size around the origin $x_1 = x_2 = 0$ asymptotically converge to the origin. We define $V(x_1,x_2)$ as

V(x_1,x_2) = \frac{g}{l} (1 - \cos x_1) + \frac{1}{2} x_2^2

This $V(x_1,x_2)$ is simply the scaled energy of the system Clearly, 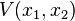$V(x_1,x_2)$ is positive definite in an open ball of radius 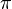$\pi$ around the origin. Computing the derivative,

\dot{V}(x_1,x_2) = \frac{g}{l} \sin x_1 \dot{x}_1 + x_2 \dot{x}_2 = - \frac{k}{m} x_2^2

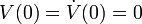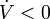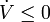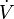Observe that $V(0) = \dot{V}(0) = 0$ . If it were true that $\dot{V} < 0$ , we could conclude that every trajectory approaches the origin by Lyapunov's second theorem. Unfortunately, $\dot{V} \leq 0$ and $\dot{V}$ is only negative semidefinite. However, the set

S = \{ (x_1,x_2) | \dot{V}(x_1,x_2) = 0 \}

which is simply the set

S = \{ (x_1,x_2) | x_2 = 0 \}

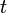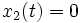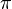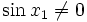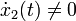does not contain any trajectory of the system, except the trivial trajectory x = 0. Indeed, if at some time $t$ , $x_2(t)=0$ , then because $x_1$ must be less than $\pi$ away from the origin, $\sin x_1 \neq 0$ and $\dot{x}_2(t) \neq 0$ . As a result, the trajectory will not stay in the set $S$ .

All the conditions of the local Krasovskii–LaSalle principle are satisfied, and we can conclude that every trajectory that begins in some neighborhood of the origin will converge to the origin as 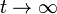$t \rightarrow \infty$ .

History

While LaSalle was the first author in the West to publish this theorem in 1960, its first publication was in 1952 by Barbashin and Krasovskii in a special case, and in 1959 by Krasovskii in the general case .

Original papers

Barbashin, E. A.; Nikolai N. Krasovskii (1952). Об устойчивости движения в целом [On the stability of motion as a whole]. Doklady Akademii Nauk SSSR (in Russian) 86: 453–456.
Krasovskii, N. N. Problems of the Theory of Stability of Motion, (Russian), 1959. English translation: Stanford University Press, Stanford, CA, 1963.
LaSalle, J.P. Some extensions of Liapunov's second method, IRE Transactions on Circuit Theory, CT-7, pp. 520–527, 1960.

Text books

Teschl, G. (2012). Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.
Wiggins, S. (2003). Introduction to Applied Nonlinear Dynamical Systems and Chaos (2 ed.). New York: Springer Verlag. ISBN 0-387-00177-8.

References

^ Lecture notes on nonlinear control, University of Notre Dame, Instructor: Michael Lemmon, lecture 4.
^ ibid.
^ Lecture notes on nonlinear analysis, National Taiwan University, Instructor: Feng-Li Lian, lecture 4-2.
^ Vidyasagar, M. Nonlinear Systems Analysis, SIAM Classics in Applied Mathematics, SIAM Press, 2002.

↑ Khalil, Hasan (2002). Nonlinear Systems (3rd ed.). Upper Saddle River NJ: Prentice Hall.