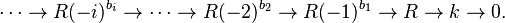Koszul algebra

In abstract algebra, a Koszul algebra $R$ is a graded $k$ -algebra over which the ground field $k$ has a linear minimal graded free resolution, i.e., there exists an exact sequence:

\cdots \rightarrow R(-i)^{b_i} \rightarrow \cdots \rightarrow R(-2)^{b_2} \rightarrow R(-1)^{b_1} \rightarrow R \rightarrow k \rightarrow 0.

It is named after the French mathematician Jean-Louis Koszul.

We can choose bases for the free modules in the resolution; then the maps can be written as matrices. For a Koszul algebra, the entries in the matrices are zero or linear forms.

An example of a Koszul algebra is a polynomial ring over a field, for which the Koszul complex is the minimal graded free resolution of the ground field. There are Koszul algebras whose ground fields have infinite minimal graded free resolutions, e.g, $R = k[x,y]/(xy)$

References

R. Froberg, Koszul Algebras, In: Advances in Commutative Ring Theory. Proceedings of the 3rd International Conference, Fez, Lect. Notes Pure Appl. Math. 205, Marcel Dekker, New York, 1999, pp. 337–350.
J.-L. Loday, B. Vallette Algebraic Operads, Springer, 2012.
A. Beilinson, V. Ginzburg, W. Soergel, "Koszul duality patterns in representation theory", J. Amer. Math. Soc. 9 (1996) 473–527.
V. Mazorchuk, S. Ovsienko, C. Stroppel, "Quadratic duals, Koszul dual functors, and applications", Trans. of the AMS 361 (2009) 1129-1172.

Koszul algebra

See also

References