Kosnita's theorem

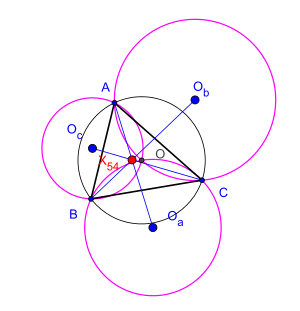
X(54) is Kosnita point of the triangle ABC

In Euclidean geometry, Kosnita's theorem is a property of certain circles associated with an arbitrary triangle.

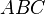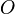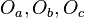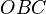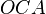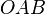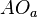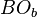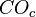Let ABC be an arbitrary triangle, O its circumcenter and O_a,O_b,O_c are the circumcenters of three triangles OBC, OCA, and OAB respectively. The theorem claims that the three straight lines AO_a, BO_b, and CO_c are concurrent.[1]

Their point of concurrence is known as the triangle's Kosnita point (named by Rigby in 1997). It is the isogonal conjugate of the nine-point center.[2][3][4] It is triangle center 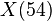X(54) in Clark Kimberling's list.[5]

References

  1. ↑ Eric W. Weisstein, Kosnita Theorem at Mathworld. Accessed on 2014-10-08.
  2. ↑ Darij Grinberg (2003), On the Kosnita Point and the Reflection Triangle. Forum Geometricorum, volume 3, pages 105–111. ISSN 1534-1178
  3. ↑ John Rigby (1997), Brief notes on some forgotten geometrical theorems. Mathematics and Informatics Quarterly, volume 7, pages 156-158 (as cited by Kimberling).
  4. ↑ Jean-Louis Ayme (), le point de Kosnitza. Online document, accessed on 2014-10-05.
  5. ↑ Clark Kimberling (2014), Encyclopedia of Triangle Centers, section X(54) = Kosnita Point. Accessed on 2014-10-08