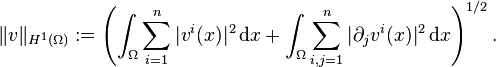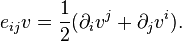Korn's inequality

In mathematical analysis, Korn's inequality is an inequality concerning the gradient of a vector field that generalizes the following classical theorem: if the gradient of a vector field is skew-symmetric at every point, then the gradient must be equal to a constant skew-symmetric matrix. Korn's theorem is a quantitative version of this statement, which intuitively says that if the gradient of a vector field is on average not far from the space of skew-symmetric matrices, then the gradient must not be far from a particular skew-symmetric matrix. The statement that Korn's inequality generalizes thus arises as a special case of rigidity.

In (linear) elasticity theory, the symmetric part of the gradient is a measure of the strain that an elastic body experiences when it is deformed by a given vector-valued function. The inequality is therefore an important tool as an a priori estimate in linear elasticity theory.

Statement of the inequality

Let Ω be an open, connected domain in n-dimensional Euclidean space Rn, n ≥ 2. Let H1(Ω) be the Sobolev space of all vector fields v = (v1, ..., vn) on Ω that, along with their weak derivatives, lie in the Lebesgue space L2(Ω). Denoting the partial derivative with respect to the ith component by ∂i, the norm in H1(Ω) is given by

\| v \|_{H^{1} (\Omega)} := \left( \int_{\Omega} \sum_{i = 1}^{n} | v^{i} (x) |^{2} \, \mathrm{d} x+\int_{\Omega} \sum_{i, j = 1}^{n} | \partial_{j} v^{i} (x) |^{2} \, \mathrm{d} x \right)^{1/2}.

Then there is a constant C ≥ 0, known as the Korn constant of Ω, such that, for all v ∈ H1(Ω),

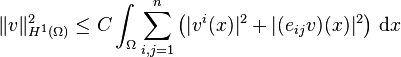
\| v \|_{H^{1} (\Omega)}^{2} \leq C \int_{\Omega} \sum_{i, j = 1}^{n} \left( | v^{i} (x) |^{2} + | (e_{ij} v) (x) |^{2} \right) \, \mathrm{d} x

 

 

 

 

(1)

where e denotes the symmetrized gradient given by

e_{ij} v = \frac1{2} ( \partial_{i} v^{j} + \partial_{j} v^{i} ).

Inequality (1) is known as Korn's inequality.

See also

References

External links