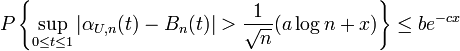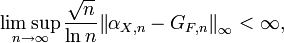Komlós–Major–Tusnády approximation

In theory of probability, the Komlós–Major–Tusnády approximation (also known as the KMT approximation, the KMT embedding, or the Hungarian embedding) is an approximation of the empirical process by a Gaussian process constructed on the same probability space. It is named after Hungarian mathematicians János Komlós, Gábor Tusnády, and Péter Major.

Theory

Let 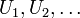U_1,U_2,\ldots be independent uniform (0,1) random variables. Define a uniform empirical distribution function as

F_{U,n}(t)=\frac{1}{n}\sum_{i=1}^n \mathbf{1}_{U_i\leq t},\quad t\in [0,1].

Define a uniform empirical process as

\alpha_{U,n}(t)=\sqrt{n}(F_{U,n}(t)-t),\quad t\in [0,1].

The Donsker theorem (1952) shows that 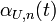\alpha_{U,n}(t) converges in law to a Brownian bridge 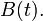B(t). Komlós, Major and Tusnády established a sharp bound for the speed of this weak convergence.

Theorem (KMT, 1975) On a suitable probability space for independent uniform (0,1) r.v. 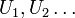U_1,U_2\ldots the empirical process 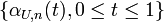\{\alpha_{U,n}(t), 0\leq t\leq 1\} can be approximated by a sequence of Brownian bridges 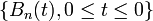\{B_n(t),0\leq t\leq 0\} such that
P\left\{\sup_{0\leq t\leq 1}|\alpha_{U,n}(t)-B_n(t)|>\frac{1}{\sqrt{n}}(a\log n+x)\right\}\leq b e^{-cx}
for all positive integers n and all x>0, where a, b, and c are positive constants.

Corollary

A corollary of that theorem is that for any real iid r.v. 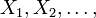X_1,X_2,\ldots, with cdf 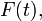F(t), it is possible to construct a probability space where independent sequences of empirical processes 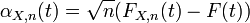\alpha_{X,n}(t)=\sqrt{n}(F_{X,n}(t)-F(t)) and Gaussian processes 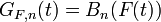G_{F,n}(t)=B_n(F(t)) exist such that

\limsup_{n\to\infty} \frac{\sqrt{n}}{\ln n} \big\| \alpha_{X,n} - G_{F,n} \big\|_\infty < \infty,     almost surely.

References