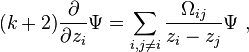Knizhnik–Zamolodchikov equations
In mathematical physics the Knizhnik–Zamolodchikov equations or KZ equations are a set of additional constraints satisfied by the correlation functions of the conformal field theory associated with an affine Lie algebra at a fixed level. They form a system of complex partial differential equations with regular singular points satisfied by the N-point functions of primary fields and can be derived using either the formalism of Lie algebras or that of vertex algebras. The structure of the genus zero part of the conformal field theory is encoded in the monodromy properties of these equations. In particular the braiding and fusion of the primary fields (or their associated representations) can be deduced from the properties of the four-point functions, for which the equations reduce to a single matrix-valued first order complex ordinary differential equation of Fuchsian type. Originally the Russian physicists Vadim Knizhnik and Alexander Zamolodchikov deduced the theory for SU(2) using the classical formulas of Gauss for the connection coefficients of the hypergeometric differential equation.
Definition
Let 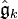 denote the affine Lie algebra with level k and dual Coxeter number h. Let v be a vector from a zero mode representation of
denote the affine Lie algebra with level k and dual Coxeter number h. Let v be a vector from a zero mode representation of  and
and 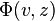 the primary field associated with it. Let
the primary field associated with it. Let 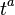 be a basis of the underlying Lie algebra
be a basis of the underlying Lie algebra 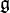 ,
, 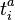 their representation on the primary field
their representation on the primary field 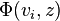 and η the Killing form. Then for
and η the Killing form. Then for 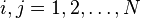 the Knizhnik–Zamolodchikov equations read
the Knizhnik–Zamolodchikov equations read
Informal derivation
The Knizhnik–Zamolodchikov equations result from the existence of null vectors in the 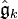 module. This is quite similar to the case in minimal models, where the existence of null vectors result in additional constraints on the correlation functions.
module. This is quite similar to the case in minimal models, where the existence of null vectors result in additional constraints on the correlation functions.
The null vectors of a 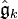 module are of the form
module are of the form
where v is a highest weight vector and 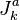 the conserved current associated with the affine generator
the conserved current associated with the affine generator 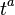 . Since v is of highest weight, the action of most
. Since v is of highest weight, the action of most 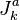 on it vanish and only
on it vanish and only 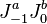 remain. The operator-state correspondence then leads directly to the Knizhnik–Zamolodchikov equations as given above.
remain. The operator-state correspondence then leads directly to the Knizhnik–Zamolodchikov equations as given above.
Mathematical formulation
Since the treatment in Tsuchiya & Kanie (1988), the Knizhnik–Zamolodchikov equation has been formulated mathematically in the language of vertex algebras due to Borcherds (1986) and Frenkel, Lepowsky & Meurman (1988). This approach was popularized amongst theoretical physicists by Goddard (1988) and amongst mathematicians by Kac (1996).
The vacuum representation H0 of an affine Kac–Moody algebra at a fixed level can be encoded in a vertex algebra. The derivation d acts as the energy operator L0 on H0, which can be written as a direct sum of the non-negative integer eigenspaces of L0, the zero energy space being generated by the vacuum vector Ω. The eigenvalue of an eigenvector of L0 is called its energy. For every state a in L there is a vertex operator V(a,z) which creates a from the vacuum vector Ω, in the sense that
The vertex operators of energy 1 correspond to the generators of the affine algebra
where X ranges over the elements of the underlying finite-dimensional simple complex Lie algebra 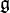 .
.
There is an energy 2 eigenvector L−2Ω which give the generators Ln of the Virasoro algebra associated to the Kac–Moody algebra by the Segal–Sugawara construction
If a has energy α, then the corresponding vertex operator has the form
The vertex operators satisfy
as well as the locality and associativity relations
These last two relations are understood as analytic continuations: the inner products with finite energy vectors of the three expressions define the same polynomials in z±1, w±1 and (z − w)−1 in the domains |z| < |w|, |z| > |w| and |z – w| < |w|. All the structural relations of the Kac–Moody and Virasoro algebra can be recovered from these relations, including the Segal–Sugawara construction.
Every other integral representation Hi at the same level becomes a module for the vertex algebra, in the sense that for each a there is a vertex operator Vi(a, z) on Hi such that
The most general vertex operators at a given level are intertwining operators Φ(v, z) between representations Hi and Hj where v lies in Hk. These operators can also be written as
but δ can now be rational numbers. Again these intertwining operators are characterized by properties
and relations with L0 and L−1 similar to those above.
When v is in the lowest energy subspace for L0 on Hk, an irreducible representation of 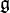 , the operator Φ(v, w) is called a primary field of charge k.
, the operator Φ(v, w) is called a primary field of charge k.
Given a chain of n primary fields starting and ending at H0, their correlation or n-point function is defined by
In the physics literature the vi are often suppressed and the primary field written Φi(zi), with the understanding that it is labelled by the corresponding irreducible representation of 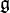 .
.
Vertex algebra derivation
If (Xs) is an orthonormal basis of 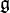 for the Killing form, the Knizhnik–Zamolodchikov equations may be deduced by integrating the correlation function
for the Killing form, the Knizhnik–Zamolodchikov equations may be deduced by integrating the correlation function
first in the w variable around a small circle centred at z; by Cauchy's theorem the result can be expressed as sum of integrals around n small circles centred at the zj's:
Integrating both sides in the z variable about a small circle centred on zi yields the ith Knizhnik–Zamolodchikov equation.
Lie algebra derivation
It is also possible to deduce the Knizhnik–Zamodchikov equations without explicit use of vertex algebras. The termΦ(vi, zi) may be replaced in the correlation function by its commutator with Lr where r = 0, ±1. The result can be expressed in terms of the derivative with respect to zi. On the other hand Lr is also given by the Segal–Sugawara formula:
After substituting these formulas for Lr, the resulting expressions can be simplified using the commutator formulas
Original derivation
The original proof of Knizhnik & Zamolodchikov (1984), reproduced in Tsuchiya & Kanie (1988), uses a combination of both of the above methods. First note that for X in 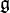
Hence
On the other hand
so that
The result follows by using this limit in the previous equality.
Monodromy representation of KZ equation
In conformal field theory along the above definition the n-point correlation function of the primary field satisfies KZ equation. In particular, for 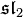 and non negative integers k there are k + 1 primary fields
and non negative integers k there are k + 1 primary fields 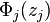 's corresponding to spin j representation ( j = 0, 1/2, 1, 3/2,.., k/2). The correlation function
's corresponding to spin j representation ( j = 0, 1/2, 1, 3/2,.., k/2). The correlation function 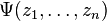 of the primary fields
of the primary fields 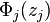 's for the representation
's for the representation 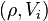 takes values in the tensor product
takes values in the tensor product 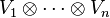 and its KZ equation is
and its KZ equation is
where 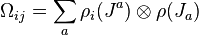 as the above informal derivation.
as the above informal derivation.
This n-point correlation function can be analytically continued as multi-valued holomorphic function to the domain 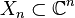 with
with 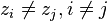 . Due to this analytic continuation the holonomy of KZ equation can be described by the braid group
. Due to this analytic continuation the holonomy of KZ equation can be described by the braid group 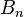 introduced by Emil Artin.Kohno (2002) In general, A complex semi-simple Lie algebra
introduced by Emil Artin.Kohno (2002) In general, A complex semi-simple Lie algebra 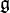 and its representations
and its representations 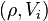 give the linear representation of braid group
give the linear representation of braid group
as the holonomy of KZ equation. Oppositely, a KZ equation gives the linear representation of braid groups as its holonomy.
The action on 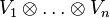 by the analytic continuation of KZ equation is called monodromy representation of KZ equation. In particular, if all
by the analytic continuation of KZ equation is called monodromy representation of KZ equation. In particular, if all 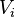 's have spin 1/2 representation then the linear representation obtained from KZ equation agrees with the representation constructed from operator algebra theory by Vaughan Jones. It is known that the monodromy representation of KZ equation with a general semi-simple Lie algebra agrees with the linear representation of braid group given by R-matrix of the corresponding quantum group.
's have spin 1/2 representation then the linear representation obtained from KZ equation agrees with the representation constructed from operator algebra theory by Vaughan Jones. It is known that the monodromy representation of KZ equation with a general semi-simple Lie algebra agrees with the linear representation of braid group given by R-matrix of the corresponding quantum group.
Applications
- Representation theory of Affine Lie algebra and quantum groups
- Braid groups
- Topology of hyperplane complements
- Knot theory and 3-folds
See also
References
- Baik, Jinho; Deift, Percy, and Johansson, Kurt (June 1999). "On the distribution of the length of the longest increasing subsequence of random permutations". J. Amer. Math. Soc. 12 (4): 1119–1178. Retrieved 5 December 2012.
- Knizhnik, V.G.; Zamolodchikov, A.B. (1984), "Current Algebra and Wess–Zumino Model in Two-Dimensions", Nucl. Phys. B 247: 83–103, Bibcode:1984NuPhB.247...83K, doi:10.1016/0550-3213(84)90374-2
- Tsuchiya, A.; Kanie, Y. (1988), Vertex operators in conformal field theory on P(1) and monodromy representations of braid group, Adv. Stud. Pure Math. 16, pp. 297–372 (Erratum in volume 19, pp. 675–682.)
- Borcherds, Richard (1986), "Vertex algebras, Kac–Moody algebras, and the Monster", Proc. Natl. Acad. Sci. USA. 83: 3068–3071, Bibcode:1986PNAS...83.3068B, doi:10.1073/pnas.83.10.3068, PMC 323452, PMID 16593694
- Frenkel, Igor; Lepowsky, James; Meurman, Arne (1988), Vertex operator algebras and the Monster, Pure and Applied Mathematics 134, Academic Press, ISBN 0-12-267065-5
- Goddard, Peter (1989), Meromorphic conformal field theory, Adv. Series in Mathematical Physics 7, World Scientific, pp. 556–587
- Kac, Victor (1998), Vertex algebras for beginners, University Lecture Series 10, American Mathematical Society, ISBN 0-8218-0643-2
- Etingof, Pavel I.; Frenkel, Igor; Kirillov, Alexander A. (1998), Lectures on Representation Theory and Knizhnik–Zamolodchikov Equations, Mathematical Surveys and Monographs 58, American Mathematical Society, ISBN 0821804960
- Frenkel, Edward; Ben-Zvi, David (2001), Vertex algebras and Algebraic Curves, Mathematical Surveys and Monographs 88, American Mathematical Society, ISBN 0-8218-2894-0
- Kohno, Toshitake (2002), Conformal Field Theory and Topology, Translation of Mathematical Monographs 210, American Mathematical Society, ISBN 978-0821821305
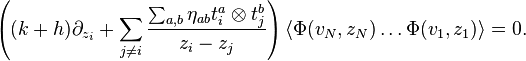
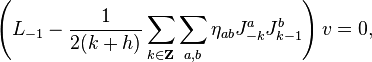
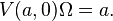
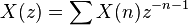
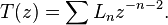
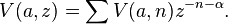
![\begin{align}
\frac{d}{dz} V(a,z) &= \left [L_{-1},V(a,z) \right ]= V \left (L_{-1}a,z \right ) \\
\left [L_0,V(a,z) \right ] &= \left (z^{-1} \frac{d}{dz} + \alpha \right )V(a,z)
\end{align}](../I/m/4c1afbdfc8a14a7b904a9a28133c1765.png)
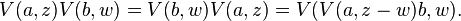
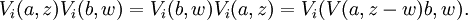
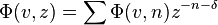
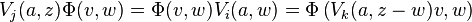
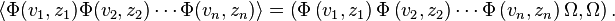
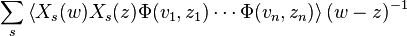
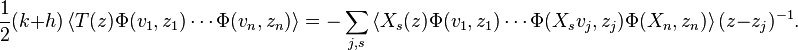
![\begin{align}
L_0 &= (k+h)^{-1}\sum_s\left[ \frac{1}{2}X_s(0)^2 + \sum_{m>0} X_s(-m)X_s(m)\right] \\
L_{\pm 1 } &=(k+h)^{-1} \sum_s\sum_{ m\ge 0} X_s(-m\pm 1)X_s(m)
\end{align}](../I/m/5a1a2f8008c0151ef3f6f485d3366b3c.png)
![[X(m),\Phi(a,n)]= \Phi(Xa,m+n).](../I/m/e17a91ee8bc2cf8891b773b0f522dc3e.png)
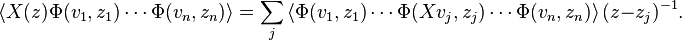
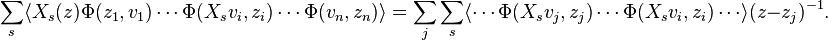
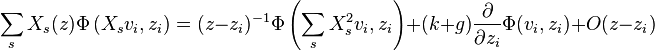
![(k+g)\frac{\partial}{\partial z_i} \Phi(v_i,z_i) = \lim_{z\to z_i} \left[\sum_s X_s(z)\Phi \left (X_sv_i,z_i \right ) -(z-z_i)^{-1}\Phi \left (\sum_s X_s^2 v_i,z_i \right )\right].](../I/m/54e8c561bf5ae1d36abeecbed9840a30.png)