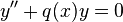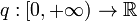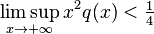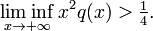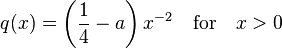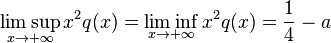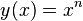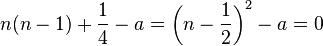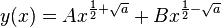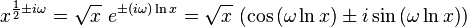Kneser's theorem (differential equations)

In mathematics, in the field of ordinary differential equations, the Kneser theorem, named after Adolf Kneser, provides criteria to decide whether a differential equation is oscillating or not.

Statement of the theorem

Consider an ordinary linear homogeneous differential equation of the form

y'' + q(x)y = 0\,

with

q: [0,+\infty) \to \mathbb{R}

continuous. We say this equation is oscillating if it has a solution y with infinitely many zeros, and non-oscillating otherwise.

The theorem states^[1] that the equation is non-oscillating if

\limsup_{x \to +\infty} x^2 q(x) < \tfrac{1}{4}

and oscillating if

\liminf_{x \to +\infty} x^2 q(x) > \tfrac{1}{4}.

Example

To illustrate the theorem consider

q(x) = \left(\frac{1}{4} - a\right) x^{-2} \quad\text{for}\quad x > 0

where $a$ is real and non-zero. According to the theorem, solutions will be oscillating or not depending on whether $a$ is positive (non-oscillating) or negative (oscillating) because

\limsup_{x \to +\infty} x^2 q(x) = \liminf_{x \to +\infty} x^2 q(x) = \frac{1}{4} - a

To find the solutions for this choice of 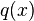$q(x)$ , and verify the theorem for this example, substitute the 'Ansatz'

y(x) = x^n \,

which gives

n(n-1) + \frac{1}{4} - a = \left(n-\frac{1}{2}\right)^2 - a = 0

This means that (for non-zero $a$ ) the general solution is

y(x) = A x^{\frac{1}{2} + \sqrt{a}} + B x^{\frac{1}{2} - \sqrt{a}}

where $A$ and $B$ are arbitrary constants.

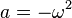It is not hard to see that for positive $a$ the solutions do not oscillate while for negative $a = -\omega^2$ the identity

x^{\frac{1}{2} \pm i \omega} = \sqrt{x}\ e^{\pm (i\omega) \ln{x}} = \sqrt{x}\ (\cos{(\omega \ln x)} \pm i \sin{(\omega \ln x)})

shows that they do.

The general result follows from this example by the Sturm–Picone comparison theorem.

Extensions

There are many extensions to this result. For a recent account see.^[2]

References

↑ Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.
↑ Helge Krüger and Gerald Teschl, Effective Prüfer angles and relative oscillation criteria, J. Diff. Eq. 245 (2008), 3823–3848