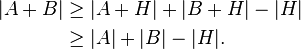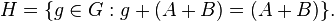Kneser's theorem (combinatorics)

In mathematics, Kneser's theorem is an inequality among the sizes of certain sumsets in finite abelian groups. It belongs to the field of additive combinatorics, and is named after Martin Kneser, who published it in 1953.^[1] It may be regarded as an extension of the Cauchy–Davenport theorem, which also concerns sumsets in groups but is restricted to groups whose order is a prime number.^[2]

Statement

Let G be a non-trivial abelian group and A, B finite non-empty subsets. If |A| + |B| ≤ |G| then there is a finite subgroup H of G such that^[3]

\begin{align} |A+B| &\ge |A+H| + |B+H| - |H| \\ &\ge |A| + |B| - |H|. \end{align}

The subgroup H can be taken to be the stabiliser^[2] of A+B

H = \lbrace g \in G : g + (A+B) = (A+B) \rbrace.

Notes

↑ Kneser, Martin (1953). "Abschätzungen der asymptotischen Dichte von Summenmengen". Math. Zeitschr. (in German) 58: 459–484. Zbl 0051.28104.
↑ 2.0 2.1 Geroldinger & Rusza (2009) p.143
↑ Tao & Vu 2010, pg. 200, Theorem 5.5

References

Geroldinger, Alfred; Ruzsa, Imre Z., eds. (2009). Combinatorial number theory and additive group theory. Advanced Courses in Mathematics CRM Barcelona. Elsholtz, C.; Freiman, G.; Hamidoune, Y. O.; Hegyvári, N.; Károlyi, G.; Nathanson, M.; Solymosi, J.; Stanchescu, Y. With a foreword by Javier Cilleruelo, Marc Noy and Oriol Serra (Coordinators of the DocCourse). Basel: Birkhäuser. ISBN 978-3-7643-8961-1. Zbl 1177.11005.
Nathanson, Melvyn B. (1996). Additive Number Theory: Inverse Problems and the Geometry of Sumsets. Graduate Texts in Mathematics 165. Springer-Verlag. pp. 109–132. ISBN 0-387-94655-1. Zbl 0859.11003.
Tao, Terence; Vu, Van H. (2010), Additive Combinatorics, Cambridge: Cambridge University Press, ISBN 978-0-521-13656-3, Zbl 1179.11002