Klincewicz method

Principle of a Group Contribution Method

In thermodynamic theory, the Klincewicz method^[1] is a predictive method based both on group contributions and on a correlation with some basic molecular properties. The method estimates the critical temperature, the critical pressure, and the critical volume of pure components.

Model description

As a group contribution method the Klincewicz method correlates some structural information of a chemical molecule with the critical data. The used structural information are small functional groups which are assumed to have no interactions. This assumption makes it possible to calculate the thermodynamic properties directly from the sums of the group contributions. The correlation method does not even use these functional groups, only the molecular weight and the number of atoms are used as molecular descriptors.

The prediction of the critical temperature relies on the knowledge of the normal boiling point because the method only predicts the relation of the normal boiling point and the critical temperature and not directly the critical temperature. The critical volume and pressure however are directly predicted.

Model Quality

The quality of the Klincewicz method is not superior to older methods, especially the method of Ambrose^[2] gives somewhat better results as stated by the original authors and by Reid et al.^[3] The advantage of the Klincewicz method is that it is less complex.

The quality and complexity of the Klincewicz method is comparable to the Lydersen method^[4] from 1955 which has been used widely in chemical engineering.

The aspect where the Klincewicz method is unique and useful^[3] are the alternative equations where only very basic molecular data like the molecular weight and the atom count are used.

Deviation diagrams

The diagrams show estimated critical data of hydrocarbons together with experimental data.^[5] An estimation would be perfect if all data points would lie directly on the diagonal line. Only the simple correlation of the Klincewicz method with the moelcular weight and the atom count have been used in this example.

Critical temperatures
Critical pressures
Critical volumes

Equations

Klincewicz published two sets of equations.^[6] The first uses contributions of 35 different groups. These group contribution based equations are giving somewhat better results than the very simple equations based only on correlations with the molecular weight and the atom count.

Group-contribution-based equations

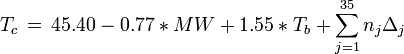
$T_c \, = \, 45.40 - 0.77 * MW + 1.55 * T_b+\sum_{j=1}^{35} n_j \Delta_j$

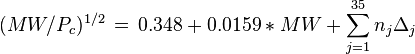
$(MW/P_c)^{1/2} \, = \, 0.348 + 0.0159 * MW + \sum_{j=1}^{35} n_j \Delta_j$

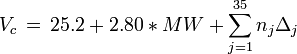
$V_c \, = \, 25.2 + 2.80 * MW + \sum_{j=1}^{35} n_j \Delta_j$

Equations based on correlation with molecular weight and atom count only

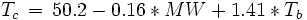
$T_c \, = \, 50.2 - 0.16 * MW + 1.41 * T_b$

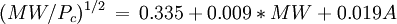
$(MW/P_c)^{1/2} \, = \, 0.335 + 0.009 * MW + 0.019A$

$V_c \, = \, 20.1 + 0.88 * MW + 13.4 * A$

with

MW:	Molecular weight in ^g/_mol
T_b:	Normal boiling point in K
A:	Number of atoms

Group contributions

	Δ_jValues for
	T_c	P_c	V_c
-CH₃	-2.433	0.026	16.2
-CH₂-	0.353	-0.015	16.1
-CH₂- (Ring)	4.253	-0.046	8.2
>CH-	6.266	-0.083	12.1
>CH- (Ring)	-0.335	-0.027	7.4
>C<	16.416	-0.136	8.95
>C< (Ring)	12.435	-0.111	-6.6
=CH₂	-0.991	-0.015	13.9
=CH-	3.786	-0.050	9.8
=CH- (Ring)	3.373	-0.066	5.1
>C=;=C=	7.169	-0.067	2.7
>C= (Ring)	5.623	-0.089	0.2
≡CH	-4.561	-0.056	7.5
≡C-	7.341	-0.112	3.0
-OH	-28.930	-0.190	-24.0
-O-	5.389	-0.143	-26.1
-O- (Ring)	7.127	-0.116	-36.6
>CO;-CHO	4.332	-0.196	-6.7
-COOH	-25.085	-0.251	-37.0
-CO-O-	8.890	-0.277	-28.2
-NH₂	-4.153	-0.127	-0.1
>NH	2.005	-0.180	53.7
>NH (Ring)	2.773	-0.172	-8.0
>N-	12.253	-0.163	-0.7
=N- (Ring)	8.239	-0.104	-18.4
-CN	-10.381	-0.064	12.0
-SH	28.529	-0.303	-27.7
-S-	23.905	-0.311	-27.3
-S- (Ring)	31.537	-0.208	-61.9
-F	5.191	-0.067	-34.1
-Cl	18.353	-0.244	-47.4
-Br	53.456	-0.692	-148.1
-I	94.186	-1.051	-270.6
-XCX (X = halogen)	-1.770	0.032	0.8
-NO₂	11.709	-0.325	-39.2

The group XCX is used to take the pairwise interaction of halogens connected to a single carbon into account. Its contribution has to be added once for two halogens but three times for three halogens (interactions between the halogens 1 and 2, 1 and 3, and 2 and 3).

Example calculations

Example calculation for acetone with group contributions

	-CH₃		>C=O (nonring)
Property	No. of groups	Group value	No. of groups	Group value	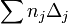$\sum n_j\Delta_j$	Estimated Value	Unit
T_c	2	-2.433	1	4.332	-0.534	510.4819*	K
P_c	2	0.026	1	-0.196	-0.144	45.69	bar
V_c	2	16.2	1	-6.7	25.7	213.524	cm³/mol

*used normal boiling point T_b= 329.250 K

Example calculation for acetone with molecular weight and atom count only

Used molecular weight: 58.080 ^g/_mol

Used atom count: 10

Property	Estimated Value	Unit
T_c	505.1497	K
P_c	52.9098	bar
V_c	205.2	cm³/mol

For comparison, experimental values for Tc, Pc and Vc are 508.1 K, 47.0 bar and 209 cm³/mol, respectively.^[3]

References

↑ Klincewicz K. M., Reid R. C., "Estimation of Critical Properties with Group Contribution Methods", AIChE Journal, 30(1), 137-142, 1984
↑ Ambrose D., "Correlation and Estimation of Vapour-Liquid Critical Properties. I. Critical Temperatures of Organic Compounds", Nat. Phys. Lab. Rep. Chem., Rep. No. NPL Rep. Chem. 92, 1-35, 1978
↑ 3.0 3.1 3.2 Reid R.C., Prausnitz J.M., Poling B.E., "The Properties of Gases & Liquids", Monograph, McGraw-Hill, 4 Ed., 1-742, 1987
↑ Lydersen A.L., "Estimation of Critical Properties of Organic Compounds", University of Wisconsin College Engineering, Eng. Exp. Stn. Rep. 3, Madison, Wisconsin, 1955
↑ Dortmund Data Bank
↑ Klincewicz, K. M., “Prediction of Critical Temperatures, Pressures, and Volumes of Organic Compounds from Molecular Structure,” S.M.Thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts, 1982