Kleitman–Wang algorithms

The Kleitman–Wang algorithms are two different algorithms in graph theory solving the digraph realization problem, i.e. the question if there exists for a finite list of nonnegative integer pairs a simple directed graph such that its degree sequence is exactly this list. For a positive answer the list of integer pairs is called digraphic. Both algorithms construct a special solution if one exists or prove that one cannot find a positive answer. These constructions are based on recursive algorithms. Kleitman and Wang ^[1] gave these algorithms in 1973.

Kleitman–Wang algorithm (arbitrary choice of pairs)

The algorithm is based on the following theorem.

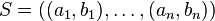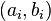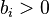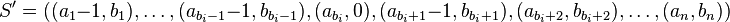Let $S=((a_1,b_1),\dots,(a_n,b_n))$ be a finite list of nonnegative integers that is in nonincreasing lexicographical order and let $(a_i,b_i)$ be a pair of nonnegative integers with $b_i >0$ . List $S$ is digraphic if and only if the finite list $S'=((a_1-1,b_1),\dots,(a_{b_i-1}-1,b_{b_i-1}),(a_{b_i},0),(a_{b_i+1}-1,b_{b_i+1}),(a_{b_i+2},b_{b_i+2}),\dots,(a_n,b_n))$ has nonnegative integer pairs and is digraphic.

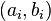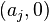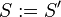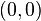Note that the pair $(a_i,b_i)$ is arbitrarily with the exception of pairs $(a_j,0)$ . If the given list $S$ digraphic then the theorem will be applied at most $n$ times setting in each further step $S:=S'$ . This process ends when the whole list $S'$ consists of $(0,0)$ pairs. In each step of the algorithm one constructs the arcs of a digraph with vertices 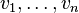$v_1,\dots,v_n$ , i.e. 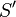if it is possible to reduce the list $S$ to $S'$ , then we add arcs 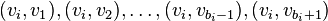$(v_i,v_1),(v_i,v_2),\dots,(v_{i},v_{b_i-1}),(v_i,v_{b_i+1})$ . 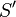When the list $S$ cannot be reduced to a list $S'$ of nonnegative integer pairs in any step of this approach, the theorem proves that the list $S$ from the beginning is not digraphic.

Kleitman–Wang algorithm (maximum choice of a pair)

The algorithm is based on the following theorem.

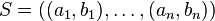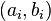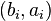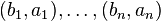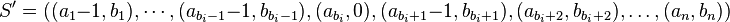Let $S=((a_1,b_1),\dots,(a_n,b_n))$ be a finite list of nonnegative integers such that $a_1 \geq a_2 \geq \cdots \geq a_n$ and let $(a_i,b_i)$ be a pair such that $(b_i,a_i)$ is maximal with respect to the lexicographical order under all pairs $(b_1,a_1),\dots,(b_n,a_n)$ . List $S$ is digraphic if and only if the finite list $S'=((a_1-1,b_1),\cdots,(a_{b_i-1}-1,b_{b_i-1}),(a_{b_i},0),(a_{b_i+1}-1,b_{b_i+1}),(a_{b_i+2},b_{b_i+2}),\dots,(a_n,b_n))$ has nonnegative integer pairs and is digraphic.

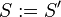Note that the list $S$ must not be in lexicographical order as in the first version. If the given list $S$ is digraphic, then the theorem will be applied at most $n$ times, setting in each further step $S:=S'$ . This process ends when the whole list 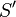$S'$ consists of 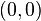$(0,0)$ pairs. In each step of the algorithm, one constructs the arcs of a digraph with vertices 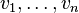$v_1,\dots,v_n$ , i.e. 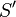if it is possible to reduce the list $S$ to $S'$ , then one adds arcs 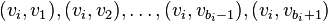$(v_i,v_1),(v_i,v_2),\dots,(v_i,v_{b_i-1}),(v_i,v_{b_i+1})$ . 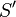When the list $S$ cannot be reduced to a list $S'$ of nonnegative integer pairs in any step of this approach, the theorem proves that the list $S$ from the beginning is not digraphic.

References

Kleitman, D. J.; Wang, D. L. (1973), "Algorithms for constructing graphs and digraphs with given valences and factors", Discrete Mathematics 6: 79–88, doi:10.1016/0012-365x(73)90037-x

↑ Kleitman (1973)

Kleitman–Wang algorithms

Kleitman–Wang algorithm (arbitrary choice of pairs)

Kleitman–Wang algorithm (maximum choice of a pair)

See also

References