Klein graphs
In the mathematical field of graph theory, the Klein graphs are two different but related regular graphs, each with 84 edges. Each can be embedded in the orientable surface of genus 3, in which they form dual graphs.
The cubic Klein graph
| Klein graph | |
|---|---|
|
The (cubic) Klein graph | |
| Named after | Felix Klein |
| Vertices | 56 |
| Edges | 84 |
| Radius | 6 |
| Diameter | 6 |
| Girth | 7 |
| Automorphisms | 336 |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties |
Symmetric Cubic Hamiltonian Cayley graph |
This graph is a 3-regular graph with 56 vertices and 84 edges, named after Felix Klein.
It is a Hamiltonian graph. It has chromatic number 3, chromatic index 3, radius 6, diameter 6 and girth 7. It is also a 3-vertex-connected and a 3-edge-connected graph.
It can be embedded in the genus-3 orientable surface (which can be represented as the Klein quartic), where it forms the "Klein map" with 24 heptagonal faces, Schläfli symbol {7,3}8.
According to the Foster census, the Klein graph, referenced as F056B, is the only cubic symmetric graph on 56 vertices which is not bipartite.[1]
It can be derived from the 28-vertex Coxeter graph.[2]
Algebraic properties
The automorphism group of the Klein graph is the group PGL2(7) of order 336, which has PSL2(7) as a normal subgroup. This group acts transitively on its half-edges, so the Klein graph is a symmetric graph.
Gallery
-

Alternative drawing of the cubic Klein graph, showing that it is Hamiltonian, with chromatic index 3.
The 7-valent Klein graph
| Klein graph | |
|---|---|
|
The (7-valent) Klein graph | |
| Named after | Felix Klein |
| Vertices | 24 |
| Edges | 84 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 3 |
| Automorphisms | 336 |
| Chromatic number | 4 |
| Chromatic index | 7 |
| Properties |
Symmetric Hamiltonian |
This graph is a 7-regular graph with 24 vertices and 84 edges, named after Felix Klein.
It is a Hamiltonian graph. It has chromatic number 4, chromatic index 7, radius 3, diameter 3 and girth 3.
It can be embedded in the genus-3 orientable surface, where it forms the dual of the "Klein map", with 56 triangular faces, Schläfli symbol {3,7}8.[3]
Algebraic properties
The automorphism group of the 7-valent Klein graph is the same group of order 336 as for the cubic Klein map, likewise acting transitively on its half-edges.
The characteristic polynomial of the Klein graph is equal to 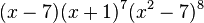 .[4]
.[4]
References
- ↑ Conder, M.; Dobcsányi, P. (2002), "Trivalent symmetric graphs up to 768 vertices", J. Combin. Math. Combin. Comput. 40: 41–63.
- ↑ Dejter, Italo. "From the Coxeter graph to the Klein graph". CiteSeer. Retrieved 23 March 2013.
- ↑ Schulte, Egon; Wills, J. M. (1985). "A Polyhedral Realization of Felix Klein's Map {3, 7}8 on a Riemann Surface of Genus 3". J. London Math. Soc. s2-32 (3).
- ↑ Weisstein, Eric. "Klein graph". MathWorld. Wolfram Research. Retrieved 23 March 2013.


