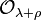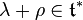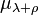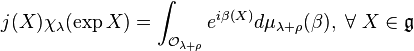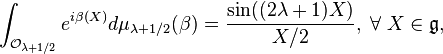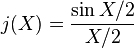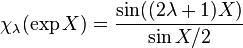Kirillov character formula
In mathematics, for a Lie group  , the Kirillov orbit method gives a heuristic method in representation theory. It connects the Fourier transforms of coadjoint orbits, which lie in the dual space of the Lie algebra of G, to the infinitesimal characters of the irreducible representations. The method got its name after the Russian mathematician Alexandre Kirillov.
, the Kirillov orbit method gives a heuristic method in representation theory. It connects the Fourier transforms of coadjoint orbits, which lie in the dual space of the Lie algebra of G, to the infinitesimal characters of the irreducible representations. The method got its name after the Russian mathematician Alexandre Kirillov.
At its simplest, it states that a character of a Lie group may be given by the Fourier transform of the Dirac delta function supported on the coadjoint orbits, weighted by the square-root of the Jacobian of the exponential map, denoted by 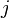 . It does not apply to all Lie groups, but works for a number of classes of connected Lie groups, including nilpotent, some semisimple groups, and compact groups.
. It does not apply to all Lie groups, but works for a number of classes of connected Lie groups, including nilpotent, some semisimple groups, and compact groups.
The Kirillov orbit method has led to a number of important developments in Lie theory, including the Duflo isomorphism and the wrapping map.
Character formula for compact Lie groups
Let  be the highest weight of an irreducible representation in the dual of the Lie algebra of the maximal torus, denoted by
be the highest weight of an irreducible representation in the dual of the Lie algebra of the maximal torus, denoted by 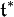 , and
, and  half the sum of the positive roots.
half the sum of the positive roots.
We denote by
the coadjoint orbit through
and
is the  -invariant measure on
-invariant measure on
with total mass
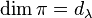 ,
,
known as the Liouville measure. If 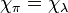 is the character of a representation, then Kirillov's character formula for compact Lie groups is then given by
is the character of a representation, then Kirillov's character formula for compact Lie groups is then given by
Example: SU(2)
For the case of SU(2), the highest weights are the positive half integers, and 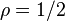 . The coadjoint orbits are the two-dimensional spheres of radius
. The coadjoint orbits are the two-dimensional spheres of radius 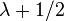 , centered at the origin in 3-dimensional space.
, centered at the origin in 3-dimensional space.
By the theory of Bessel functions, it may be shown that
and
thus yielding the characters of SU(2):
References
- Kirillov, A. A., Lectures on the Orbit Method, Graduate studies in Mathematics, 64, AMS, Rhode Island, 2004.