Kirchhoff integral theorem
Kirchhoff's integral theorem (sometimes referred to as the Fresnel-Kirchhoff integral theorem)[1] uses Green's identities to derive the solution to the homogeneous wave equation at an arbitrary point P in terms of the values of the solution of the wave equation and its first-order derivative at all points on an arbitrary surface that encloses P.[2]
Equation
Monochromatic waves
The integral has the following form for a monochromatic wave:[2][3]
where the integration is performed over an arbitrary closed surface S (enclosing r), s is the distance from the surface element to the point r, and ∂/∂n denotes differentiation along the surface normal (a normal derivative). Note that in this equation the normal points inside the enclosed volume; if the more usual outer-pointing normal is used, the integral has the opposite sign.
Non-monochromatic waves
A more general form can be derived for non-monochromatic waves. The complex amplitude of the wave can be represented by a Fourier integral of the form:
where, by Fourier inversion, we have:
The integral theorem (above) is applied to each Fourier component Uω, and the following expression is obtained:[2]
where the square brackets on V terms denote retarded values, i.e. the values at time t − s/c.
Kirchhoff showed the above equation can be approximated in many cases to a simpler form, known as the Kirchhoff, or Fresnel–Kirchhoff diffraction formula, which is equivalent to the Huygens–Fresnel equation, but provides a formula for the inclination factor, which is not defined in the latter. The diffraction integral can be applied to a wide range of problems in optics.
See also
- Kirchhoff's diffraction formula
- Vector calculus
- Integral
- Huygens–Fresnel principle
- Wavefront
- Surface
References
- ↑ G. Kirchhoff, Ann. d. Physik. 1883, 2, 18, p663
- ↑ 2.0 2.1 2.2 Max Born and Emil Wolf, Principles of Optics, 1999, Cambridge University Press, Cambridge, pp. 417-420
- ↑ Introduction to Fourier Optics J. Goodman sec. 3.3.3
Further reading
- The Cambridge Handbook of Physics Formulas, G. Woan, Cambridge University Press, 2010, ISBN 978-0-521-57507-2.
- Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007, ISBN 81-7758-293-3
- Light and Matter: Electromagnetism, Optics, Spectroscopy and Lasers, Y.B. Band, John Wiley & Sons, 2010, ISBN 978-0-471-89931-0
- The Light Fantastic – Introduction to Classic and Quantum Optics, I.R. Kenyon, Oxford University Press, 2008, ISBN 978-0-19-856646-5
- Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
- McGraw Hill Encyclopaedia of Physics (2nd Edition), C.B. Parker, 1994, ISBN 0-07-051400-3
![U(\mathbf{r}) = \frac{1}{4\pi} \int_S \left[ U \frac{\partial}{\partial\hat{\mathbf{n}}} \left( \frac{e^{iks}}{s} \right) - \frac{e^{iks}}{s} \frac{\partial U}{\partial\hat{\mathbf{n}}} \right] dS,](../I/m/9c274f3ccc75a07a57f210ea836f7165.png)
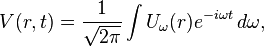
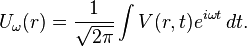
![V(r,t) = \frac{1}{4\pi} \int_S \left\{[V] \frac {\partial}{\partial n} \left(\frac {1}{s}\right) - \frac {1}{cs} \frac {\partial s}{\partial n} \left[\frac{\partial V}{\partial t}\right] - \frac{1}{s} \left[\frac{\partial V}{\partial n} \right] \right\} dS,](../I/m/9eb96dd554614891789fc9aebd701cc7.png)