Kinetic sorted list
A kinetic sorted list is a kinetic data structure for maintaining a list of points under motion in sorted order. It is used as a kinetic predecessor data structure, and as a component in more complex kinetic data structures such as kinetic closest pair.
Implementation
This data structure maintains a list of the elements in sorted order, with the certificates enforcing the order between adjacent elements. When a certificate fails, the concerned elements are swapped. Then at most three certificates must be updated, the certificate of the swapped pair, and the two certificates involving the swapped elements and the elements of the sorted list which directly precede and follow the swapped pair.
For example, given a sorted list {A,B,C,D,E,F}, the certificates will be [A<B], [B<C], [C<D], [D<E], [E<F]. If the certificate [C<D] fails, the list will be updated to {A,B,D,C,E,F}, and the certificates [B<C], [C<D], and [D<E], will be replaced with [B<D], [D<C], and [C<E], respectively. The new set of certificates will be [A<B], [B<D], [D<C], [C<E], [E<F]
Analysis
This kinetic data structure is:
- Responsive: a certificate failure causes one swap (which takes O(1) time) and O(1) certificate changes which take O(log n) time to reschedule
- Local: every element is involved in at most 2 certificates
- Compact: there are exactly n-1 certificates for a list of n elements
- Efficient: this data structure causes no extraneous internal events, every change in the ordering of the elements causes exactly one certificate failure.
Generalization
This data structure can be generalized to a kinetic data structure which can return a sorted list of points in 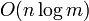 time and processes
time and processes 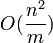 events total, assuming pseudo algebraic trajectories, where
events total, assuming pseudo algebraic trajectories, where  is a parameter of the data structure. Thus, a maintenance-time versus query-time tradeoff can be made to tune to specific applications.
is a parameter of the data structure. Thus, a maintenance-time versus query-time tradeoff can be made to tune to specific applications.
In the generalized data structure, the points are partitioned arbitrarily into m subsets of size 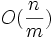 , and kinetic sorted lists are maintained on the subsets. Each sorted sublist needs to process
, and kinetic sorted lists are maintained on the subsets. Each sorted sublist needs to process 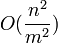 events (certificate failures) maximum, since there are
events (certificate failures) maximum, since there are 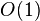 swaps of each of the
swaps of each of the 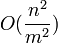 pairs of elements. Thus the total time required to maintain the data structure is
pairs of elements. Thus the total time required to maintain the data structure is 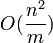 . Requests for the sorted list can then be answered in
. Requests for the sorted list can then be answered in 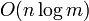 by merging the sorted sublists with mergesort.
by merging the sorted sublists with mergesort.
References
Abam, M.A., De Berg, M. Kinetic sorting and kinetic convex hulls (2007) Computational Geometry: Theory and Applications, 37 (1 SPEC. ISS.), pp. 16-26. doi: 10.1016/j.comgeo.2006.02.004