Kinetic minimum box
Kinetic minimum box is a kinetic data structure to maintain the minimum bounding box of a set of points whose positions change continuously with time. For points moving in a plane, the kinetic convex hull data structure can be used as a basis for a responsive, compact and efficient kinetic minimum box data structure.
2D case
The 2D kinetic minimum box builds on the 2D kinetic convex hull in a manner similar to the kinetic width data structure which maintains the pair of minimum-distance parallel lines that have the entire point set between them. In this case, since a box consists of two pairs of parallel lines (that are perpendicular to each other), analogy can be made with running two perpendicular kinetic width problems, and the data-structure needs to maintain sets of four points - two antipodal pairs which have perpendicular supporting lines.
In the dual view where a point (a, b) maps to a line y=ax+b, four envelopes (left, right, upper, lower) are computed. The range in x-values of a line segment in one of these envelopes corresponds to the range in the supporting slopes of the corresponding convex hull vertex in the primal view. Thus, an interval where the x-values of the four envelopes lists overlap (which can be obtained by merging the lists) corresponds, in the primal view, to a slope range where all lines parallel and perpendicular to the slopes support the same four convex hull vertices. The minimum box (in terms of area or perimeter) can be easily computed for each slope range and the four vertices thus supported, and then the global minimum box can be found by minimizing over these intervals. This algorithm can be kinetized by maintaining the convex hull in a kinetic convex hull data structure, the merge of the four envelope lists in a kinetic sorted list and the boxes in a kinetic priority queue.
Analysis
The responsiveness and compactness of this data structure follow from those of the kinetic convex hull, kinetic sorted list and kinetic priority queue data structures. This is also efficient since the number of combinatorially different minimum boxes for n points is 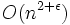 .[1] The existence of a local data structure for this problem is an open problem.
.[1] The existence of a local data structure for this problem is an open problem.
References
- ↑ Agarwal, Pankaj; Guibas, Leonidas J.; Hershberger, John; Eric Veach (1997). Maintaining the Extent of a Moving Point Set. SCG. ACM. Retrieved May 19, 2012.