Kinetic heap

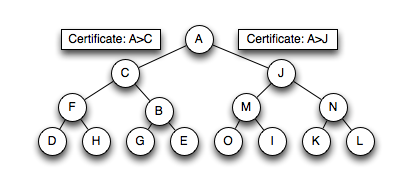
A Kinetic Heap is a kinetic data structure, obtained by the kinetization of a heap. It is designed to store elements (keys associated with priorities) where the priority is changing as a continuous function of time. As a type of kinetic priority queue, it maintains the maximum priority element stored in it. The kinetic heap data structure works by storing the elements as a tree that satisfies the following heap property - if $B$ is a child node of $A$ , then the priority of the element in $A$ must be higher than the priority of the element in $B$ . This heap property is enforced using certificates along every edge so, like other kinetic data structures, a kinetic heap also contains a priority queue (the event queue) to maintain certificate failure times.

Implementation and operations

A regular heap can be kinetized by augmenting with a certificate [ $A > B$ ] for every pair of nodes $A$ , $B$ such that $B$ is a child node of $A$ . If the value stored at a node $X$ is a function $f X (t)$ of time, then this certificate is only valid while $f A (t) > f B (t)$ . Thus, the failure of this certificate must be scheduled in the event queue at a time $t$ such that $f A (t) > f B (t)$ .

All certificate failures are scheduled on the "event queue", which is assumed to be an efficient priority queue whose operations take $O(log n)$ time.

Dealing with certificate failures

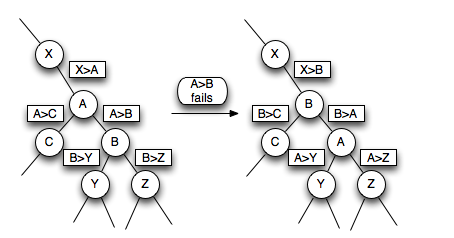
When a certificate [ $A > B$ ] fails, the data structure must swap $A$ and $B$ in the heap, and update the certificates that each of them was present in.

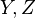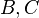For example, if $B$ (call its child nodes $Y,Z$ ) was a child node of $A$ (call its child nodes $B,C$ and its parent node $X$ ), and the certificate [ $A > B$ ] fails, then the data structure must swap $B$ and $A$ , then replace the old certificates (and the corresponding scheduled events) [ $A > B$ ], [ $A < X$ ], [ $A > C$ ], [ $B > Y$ ], [ $B > Z$ ] with new certificates [ $B > A$ ], [ $B < X$ ], [ $B > C$ ], [ $A > Y$ ] and [ $A > Z$ ].

Thus, assuming non-degeneracy of the events (no two events happen at the same time), only a constant number of events need to be de-scheduled and re-scheduled even in the worst case.

Operations

A kinetic heap supports the following operations:

$create-heap (h)$ : create an empty kinetic heap $h$
$find-max (h, t)$ (or find-min): - return the $max$ (or $min$ for a $min-heap$ ) value stored in the heap $h$ at the current virtual time $t$ .
$insert (X, f X, t)$ : - insert a key $X$ into the kinetic heap at the current virtual time $t$ , whose value changes as a continuous function $f X (t)$ of time $t$ . The insertion is done as in a normal heap in $O(log n)$ time, but $O(log n)$ certificates might need to be changed as a result, so the total time for rescheduling certificate failures is $O(log 2 n)$
$delete (X, t)$ - delete a key at the current virtual time $t$ . The deletion is done as in a normal heap in $O(log n)$ time, but $O(log n)$ certificates might need to be changed as a result, so the total time for rescheduling certificate failures is $O(log 2 n)$ .

Performance

Kinetic heaps perform well according to the four metrics (responsiveness, locality, compactness and efficiency) of kinetic data structure quality defined by Basch et al.^[1] The analysis of the first three qualities is straightforward:

Responsiveness:A kinetic heap is responsive, since each certificate failure causes the concerned keys to be swapped and leads to only five certificates being replaced in the worst case.
Locality: Each node is present in one certificate each along with its parent node and two child nodes (if present), meaning that each node can be involved in a total of three scheduled events in the worst case, thus kinetic heaps are local.
Compactness: Each edge in the heap corresponds to exactly one scheduled event, therefore the number of scheduled events is exactly where $n$ is the number of nodes in the kinetic heap. Thus, kinetic heaps are compact.

Analysis of efficiency

The efficiency of a kinetic heap in the general case is largely unknown.^[1]^[2]^[3]However, in the special case of affine motion $f(t) = a t + b$ of the priorities, kinetic heaps are known to be very efficient.^[2]

Affine motion, no insertions or deletions

In this special case, the maximum number of events processed by a kinetic heap can be shown to be exactly the number of edges in the transitive closure of the tree structure of the heap, which is $O(n log n)$ for a tree of height $O(log n)$ ^[2]

Affine motion, with insertions and deletions

If $n$ insertions and deletions are made on a kinetic heap that starts empty, the maximum number of events processed is 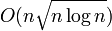$O(n \sqrt{n\log n})$ .^[4] However, this bound is not believed to be tight,^[2] and the only known lower bound is 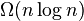$\Omega(n\log n)$ .^[4]

Variants

This article deals with "simple" kinetic heaps as described above, but other variants have been developed for specialized applications,^[5] such as:

Fibonacci kinetic heap
Incremental kinetic heap

Other heap-like kinetic priority queues are:

References

↑ 1.0 1.1 Basch, J., Guibas, L. J., Hershberger, J (1997). "Data structures for mobile data". Proceedings of the eighth annual ACM-SIAM symposium on Discrete algorithms. SODA. Society for Industrial and Applied Mathematics. pp. 747 –756. Retrieved May 17, 2012.
↑ 2.0 2.1 2.2 2.3 da Fonseca, Guilherme D. and de Figueiredo, Celina M. H. "Kinetic heap-ordered trees: Tight analysis and improved algorithms". Information Processing Letters. pp. 165–169. Retrieved May 17, 2012.
↑ da Fonseca, Guilherme D. and de Figueiredo, Celina M. H. and Carvalho, Paulo C. P. "Kinetic hanger". Information Processing Letters. pp. 151–157. Retrieved May 17, 2012.
↑ 4.0 4.1 Basch, J, Guibas, L. J., Ramkumar, G. D. (1997). "Sweeping lines and line segments with a heap". Proceedings of the thirteenth annual symposium on Computational geometry. SCG. ACM. pp. 469–471. Retrieved May 17, 2012.
↑ K. H., Tarjan, R. and T. K. (2001). "Faster kinetic heaps and their use in broadcast scheduling". Proc. 12th ACM-SIAM Symposium on Discrete Algorithms. ACM. pp. 836–844. Retrieved May 17, 2012.

Guibas, Leonidas. "Kinetic Data Structures - Handbook". Retrieved May 17, 2012.