Key derivation function

In cryptography, a key derivation function (or KDF) derives one or more secret keys from a secret value such as a master key or other known information such as a password or passphrase using a pseudo-random function.[1][2] Keyed cryptographic hash functions are popular examples of pseudo-random functions used for key derivation.[3]

Uses of KDFs

Key derivation functions are often used in conjunction with non-secret parameters to derive one or more keys from a common secret value (which is sometimes also referred to as "key diversification"). Such use may prevent an attacker who obtains a derived key from learning useful information about either the input secret value or any of the other derived keys. A KDF may also be used to ensure that derived keys have other desirable properties, such as avoiding "weak keys" in some specific encryption systems.

The most common use of KDFs is the password hashing approach to password verification, as used by the passwd file or shadow password file. KDFs happen to have the characteristics desired for a "password hash function", even though they weren't originally designed for this purpose. The non-secret parameters are called "salt" in this context. In 2013 a "Password Hashing Competition" was announced to choose a new, standard algorithm for password hashing.[4] By the second quarter of 2015, a new standard algorithm will be chosen.

Key derivation functions are often used as components of multiparty key-agreement protocols. Examples of such key derivation functions include KDF1, defined in IEEE Std 1363-2000, and similar functions in ANSI X9.42.

Key derivation functions are also used to derive keys from secret passwords or passphrases.

The "HMAC-based Extract-and-Expand Key Derivation Function" or "HKDF" specified in RFC 5869[5] is a simple HMAC-based KDF, which can be used as a building block in various protocols and applications.

Key stretching

Main article: Key stretching

Key derivation functions are also used in applications to derive keys from secret passwords or passphrases, which typically do not have the desired properties to be used directly as cryptographic keys. In such applications, it is generally recommended that the key derivation function be made deliberately slow so as to frustrate brute-force attack or dictionary attack on the password or passphrase input value.

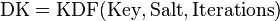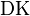Such use may be expressed as \mathrm{DK}=\mathrm{KDF}(\mathrm{Key}, \mathrm{Salt}, \mathrm{Iterations}) where \mathrm{DK} is the derived key, 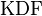\mathrm{KDF} is the key derivation function, 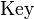\mathrm{Key} is the original key or password, 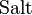\mathrm{Salt} is a random number which acts as cryptographic salt, and 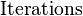\mathrm{Iterations} refers to the number of iterations of a sub-function. The derived key is used instead of the original key or password as the key to the system. The values of the salt and the number of iterations (if it isn't fixed) are stored with the hashed password or sent as plaintext with an encrypted message.[6]

The difficulty of a brute force attack increases with the number of iterations. A practical limit on the iteration count is the unwillingness of users to tolerate a perceptible delay in logging in to a computer or seeing a decrypted message. The use of salt prevents the attackers from precomputing a dictionary of derived keys.[6]

An alternative approach, called key strengthening, extends the key with a random salt, but then (unlike in key stretching) securely deletes the salt. This forces both the attacker and legitimate users to perform a brute-force search for the salt value.[7] Although the paper that introduced key stretching [8] referred to this earlier technique and intentionally chose a different name, the term "key strengthening" is now often (arguably incorrectly) used to refer to key stretching.

The first deliberately slow (key stretching) password-based key derivation function was called "crypt" (or "crypt(3)" after its man page), and was invented by Robert Morris in 1978 to encrypt Unix passwords.[9] While it was a great advance at the time, increases in processor speeds since the PDP-11 era have made brute-force attacks against crypt feasible, and advances in storage have rendered the 12-bit salt inadequate. The crypt function's design also limits the user password to 8 characters, which limits the keyspace and makes strong passphrases impossible.

Modern password-based key derivation functions, such as PBKDF2 (specified in RFC 2898), use a cryptographic hash, such as MD5 or SHA1, more salt (e.g. 64 bits and greater) and a high iteration count (often 1000 or more). NIST requires at least 128 bits of random salt and a NIST-approved cryptographic function, such as the SHA series or AES (MD5 is not approved).[10] There have been proposals to use algorithms that require large amounts of computer memory and other computing resources to make custom hardware attacks more difficult to mount. One concrete instance of such an algorithm is the scrypt function, based on the concept of sequential memory-hard functions,[11] which is used for additional securing private keys by passphrase in the tarsnap backup system.

See also

References

  1. ↑ Bezzi, Michele et al. (2011). "Data privacy". In Camenisch, Jan et al. Privacy and Identity Management for Life. Springer. pp. 185–186. ISBN 9783642203176.
  2. ↑ Kaliski, Burt; RSA Laboratories. "RFC 2898 -- PKCS #5: Password-Based Cryptography Specification, Version 2.0". IETF.
  3. ↑ Zdziarski, Jonathan (2012). Hacking and Securing IOS Applications: Stealing Data, Hijacking Software, and How to Prevent It. O'Reilly Media. pp. 252–253. ISBN 9781449318741.
  4. ↑ "Call for submissions". Password Hashing Competition. Retrieved 29 January 2015.
  5. ↑ Krawczyk, H. & Eronen, P. (May 2010). "RFC 5869 -- HMAC-based Extract-and-Expand Key Derivation Function (HKDF)". IETF.
  6. ↑ 6.0 6.1 "Salted Password Hashing - Doing it Right". CrackStation.net. Retrieved 29 January 2015.
  7. ↑ U. Manber, "A Simple Scheme to Make Passwords Based on One-Way Functions Much Harder to Crack," Computers & Security, v.15, n.2, 1996, pp.171-176.
  8. ↑ Secure Applications of Low-Entropy Keys, J. Kelsey, B. Schneier, C. Hall, and D. Wagner (1997)
  9. ↑ Morris, Robert; Thompson, Ken (1978-04-03). "Password Security: A Case History.". Bell Laboratories. Retrieved 2011-05-09.
  10. ↑ NIST SP 800-132 Section 5.1
  11. ↑ http://www.tarsnap.com/scrypt/

Further reading