Key-independent optimality
Key-independent optimality is a property of some binary search tree data structures in computer science proposed by John Iacono.[1] Suppose that key-value pairs are stored in a data structure, and that the keys have no relation to their paired values. A data structure has **key-independent optimality** if, when randomly assigning the keys, the expected performance of the data structure is within a constant factor of the optimal data structure. Key-independent optimality is related to dynamic optimality.
Definitions
There are many binary search tree algorithms that
can look up a sequence of  keys
keys 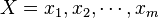 , where each
, where each 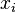 is a number between
is a number between 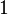 and
and  .
For each sequence
.
For each sequence  , let
, let 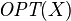 be the fastest binary search tree algorithm that looks up the elements in
be the fastest binary search tree algorithm that looks up the elements in  in order.
Let
in order.
Let  be one of the
be one of the
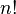 possible
permutation of the sequence
possible
permutation of the sequence  , chosen at random,
where
, chosen at random,
where
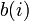 is the
is the  th entry of
th entry of  .
Let
.
Let 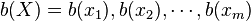 .
Iacono defined, for a sequence
.
Iacono defined, for a sequence  , that
, that ![\textit{KIOPT}(X) =
E[\textit{OPT}(b(X))]](../I/m/9c9d78071f5ce4d330a661c7d791307a.png) .
.
A data structure has key-independent optimality
if it can lookup the elements in  in time
in time
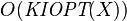 .
.
Relationship with other bounds
Key-independent optimality has been proved to be asymptotically equivalent to the working set theorem. Splay trees are known to have key-independent optimality.