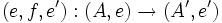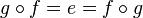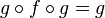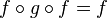Karoubi envelope
In mathematics the Karoubi envelope (or Cauchy completion or idempotent completion) of a category C is a classification of the idempotents of C, by means of an auxiliary category. Taking the Karoubi envelope of a preadditive category gives a pseudo-abelian category, hence the construction is sometimes called the pseudo-abelian completion. It is named for the French mathematician Max Karoubi.
Given a category C, an idempotent of C is an endomorphism
with
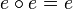 .
.
An idempotent e: A → A is said to split if there is an object B and morphisms f: A → B, g : B → A such that e = g f and 1B = f g.
The Karoubi envelope of C, sometimes written Split(C), is the category whose objects are pairs of the form (A, e) where A is an object of C and 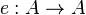 is an idempotent of C, and whose morphisms are the triples
is an idempotent of C, and whose morphisms are the triples
where 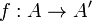 is a morphism of C satisfying
is a morphism of C satisfying 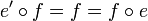 (or equivalently
(or equivalently 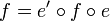 ).
).
Composition in Split(C) is as in C, but the identity morphism
on  in Split(C) is
in Split(C) is 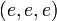 , rather than
the identity on
, rather than
the identity on  .
.
The category C embeds fully and faithfully in Split(C). In Split(C) every idempotent splits, and Split(C) is the universal category with this property. The Karoubi envelope of a category C can therefore be considered as the "completion" of C which splits idempotents.
The Karoubi envelope of a category C can equivalently be defined as the full subcategory of 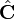 (the presheaves over C) of retracts of representable functors. The category of presheaves on C is equivalent to the category of presheaves on Split(C).
(the presheaves over C) of retracts of representable functors. The category of presheaves on C is equivalent to the category of presheaves on Split(C).
Automorphisms in the Karoubi envelope
An automorphism in Split(C) is of the form 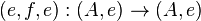 , with inverse
, with inverse 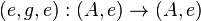 satisfying:
satisfying:
If the first equation is relaxed to just have 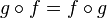 , then f is a partial automorphism (with inverse g). A (partial) involution in Split(C) is a self-inverse (partial) automorphism.
, then f is a partial automorphism (with inverse g). A (partial) involution in Split(C) is a self-inverse (partial) automorphism.
Examples
- If C has products, then given an isomorphism
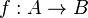 the mapping
the mapping 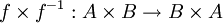 , composed with the canonical map
, composed with the canonical map 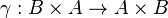 of symmetry, is a partial involution.
of symmetry, is a partial involution. - If C is a triangulated category, the Karoubi envelope Split(C) can be endowed with the structure of a triangulated category such that the canonical functor C → Split(C) becomes a triangulated functor.[1]
- The Karoubi envelope is used in the construction of several categories of motives.
- The Karoubi envelope construction takes semi-adjunctions to adjunctions.[2] For this reason the Karoubi envelope is used in the study of models of the untyped lambda calculus. The Karoubi envelope of an extensional lambda model (a monoid, considered as a category) is cartesian closed.[3][4]
References
- ↑ Balmer & Schlichting 2001
- ↑ Susumu Hayashi (1985). "Adjunction of Semifunctors: Categorical Structures in Non-extensional Lambda Calculus". Theoretical Computer Science 41: 95–104. doi:10.1016/0304-3975(85)90062-3.
- ↑ C.P.J. Koymans (1982). "Models of the lambda calculus". Information and Control 52: 306–332. doi:10.1016/s0019-9958(82)90796-3.
- ↑ DS Scott (1980). "Relating theories of the lambda calculus". To HB Curry: Essays in Combinatory Logic.
- Balmer, Paul; Schlichting, Marco (2001), "Idempotent completion of triangulated categories", Journal of Algebra 236 (2): 819–834, doi:10.1006/jabr.2000.8529, ISSN 0021-8693