Karger's algorithm
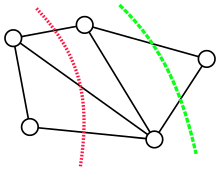
In computer science and graph theory, Karger's algorithm is a randomized algorithm to compute a minimum cut of a connected graph. It was invented by David Karger and first published in 1993.[1]
The idea of the algorithm is based on the concept of contraction of an edge 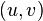 in an undirected graph
in an undirected graph 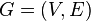 . Informally speaking, the contraction of an edge merges the nodes
. Informally speaking, the contraction of an edge merges the nodes  and
and  into one, reducing the total number of nodes of the graph by one. All other edges connecting either
into one, reducing the total number of nodes of the graph by one. All other edges connecting either  or
or  are "reattached" to the merged node, effectively producing a multigraph. Karger's basic algorithm iteratively contracts randomly chosen edges until only two nodes remain; those nodes represent a cut in the original graph. By iterating this basic algorithm a sufficient number of times, a minimum cut can be found with high probability.
are "reattached" to the merged node, effectively producing a multigraph. Karger's basic algorithm iteratively contracts randomly chosen edges until only two nodes remain; those nodes represent a cut in the original graph. By iterating this basic algorithm a sufficient number of times, a minimum cut can be found with high probability.
The global minimum cut problem
A cut 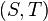 in an undirected graph
in an undirected graph 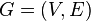 is a partition of the vertices
is a partition of the vertices  into two non-empty, disjoint sets
into two non-empty, disjoint sets 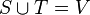 .
The cutset of a cut consists of the edges
.
The cutset of a cut consists of the edges 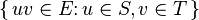 between the two parts.
The size (or weight) of a cut in an unweighted graph is the cardinality of the cutset, i.e., the number of edges between the two parts,
between the two parts.
The size (or weight) of a cut in an unweighted graph is the cardinality of the cutset, i.e., the number of edges between the two parts,
There are 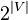 ways of choosing for each vertex whether it belongs to
ways of choosing for each vertex whether it belongs to  or to
or to  , but two of these choices make
, but two of these choices make  or
or  empty and do not give rise to cuts. Among the remaining choices, swapping the roles of
empty and do not give rise to cuts. Among the remaining choices, swapping the roles of  and
and  does not change the cut, so each cut is counted twice; therefore, there are
does not change the cut, so each cut is counted twice; therefore, there are 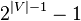 distinct cuts.
The minimum cut problem is to find a cut of smallest size among these cuts.
distinct cuts.
The minimum cut problem is to find a cut of smallest size among these cuts.
For weighted graphs with positive edge weights 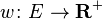 the weight of the cut is the sum of the weights of edges between vertices in each part
the weight of the cut is the sum of the weights of edges between vertices in each part
which agrees with the unweighted definition for 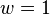 .
.
A cut is sometimes called a “global cut” to distinguish it from an “ -
- cut” for a given pair of vertices, which has the additional requirement that
cut” for a given pair of vertices, which has the additional requirement that 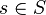 and
and 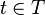 . Every global cut is an
. Every global cut is an  -
- cut for some
cut for some 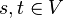 . Thus, the minimum cut problem can be solved in polynomial time by iterating over all choices of
. Thus, the minimum cut problem can be solved in polynomial time by iterating over all choices of 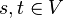 and solving the resulting minimum
and solving the resulting minimum  -
- cut problem using the max-flow min-cut theorem and a polynomial time algorithm for maximum flow, such as the Ford–Fulkerson algorithm, though this approach is not optimal. There is a deterministic algorithm for the global minimum cut problem with running time
cut problem using the max-flow min-cut theorem and a polynomial time algorithm for maximum flow, such as the Ford–Fulkerson algorithm, though this approach is not optimal. There is a deterministic algorithm for the global minimum cut problem with running time 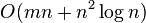 .[2]
.[2]
Contraction algorithm
The fundamental operation of Karger’s algorithm is a form of edge contraction. The result of contracting the edge 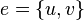 is new node
is new node 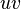 . Every edge
. Every edge 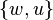 or
or 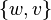 for
for 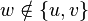 to the endpoints of the contracted edge is replaced by an edge
to the endpoints of the contracted edge is replaced by an edge 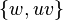 to the new node. Finally, the contracted nodes
to the new node. Finally, the contracted nodes  and
and  with all their incident edges are removed. In particular, the resulting graph contains no self-loops. The result of contracting edge
with all their incident edges are removed. In particular, the resulting graph contains no self-loops. The result of contracting edge  is denoted
is denoted 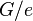 .
.
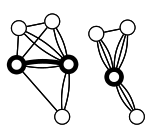
The contraction algorithm repeatedly contracts random edges in the graph, until only two nodes remain, at which point there is only a single cut.
procedure contract(): while
choose
uniformly at random
return the only cut in
When the graph is represented using adjacency lists or an adjacency matrix, a single edge contraction operation can be implemented with a linear number of updates to the data structure, for a total running time of 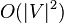 . Alternatively, the procedure can be viewed as an execution of Kruskal’s algorithm for constructing the minimum spanning tree in a graph where the edges have weights
. Alternatively, the procedure can be viewed as an execution of Kruskal’s algorithm for constructing the minimum spanning tree in a graph where the edges have weights 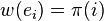 according to a random permutation
according to a random permutation 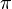 . Removing the heaviest edge of this tree results in two components that describe a cut. In this way, the contraction procedure can be implemented like Kruskal’s algorithm in time
. Removing the heaviest edge of this tree results in two components that describe a cut. In this way, the contraction procedure can be implemented like Kruskal’s algorithm in time 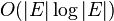 .
.
The best known implementations use 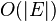 time and space, or
time and space, or 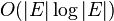 time and
time and 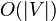 space, respectively.[1]
space, respectively.[1]
Success probability of the contraction algorithm
In a graph 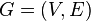 with
with  vertices, the contraction algorithm returns a minimum cut with polynomially small probability
vertices, the contraction algorithm returns a minimum cut with polynomially small probability 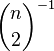 . Every graph has
. Every graph has 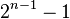 cuts,[3] among which at most
cuts,[3] among which at most 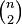 can be minimum cuts. Therefore, the success probability for this algorithm is much better than the probability for picking a cut at random, which is at most
can be minimum cuts. Therefore, the success probability for this algorithm is much better than the probability for picking a cut at random, which is at most 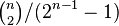
For instance, the cycle graph on  vertices has exactly
vertices has exactly 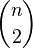 minimum cuts, given by every choice of 2 edges. The contraction procedure finds each of these with equal probability.
minimum cuts, given by every choice of 2 edges. The contraction procedure finds each of these with equal probability.
To establish the bound on the success probability in general, let  denote the edges of a specific minimum cut of size
denote the edges of a specific minimum cut of size  . The contraction algorithm returns
. The contraction algorithm returns  if none of the random edges belongs to the cutset of
if none of the random edges belongs to the cutset of  . In particular, the first edge contraction avoids
. In particular, the first edge contraction avoids  , which happens with probability
, which happens with probability 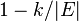 . The minimum degree of
. The minimum degree of  is at least
is at least  (otherwise a minimum degree vertex would induce a smaller cut), so
(otherwise a minimum degree vertex would induce a smaller cut), so 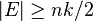 . Thus, the probability that the contraction algorithm picks an edge from
. Thus, the probability that the contraction algorithm picks an edge from  is
is
The probability 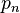 that the contraction algorithm on an
that the contraction algorithm on an  -vertex graph avoids
-vertex graph avoids  satisfies the recurrence
satisfies the recurrence 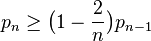 , with
, with 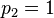 , which can be expanded as
, which can be expanded as
Repeating the contraction algorithm

By repeating the contraction algorithm 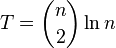 times with independent random choices and returning the smallest cut, the probability of not finding a minimum cut is
times with independent random choices and returning the smallest cut, the probability of not finding a minimum cut is
The total running time for  repetitions for a graph with
repetitions for a graph with  vertices and
vertices and  edges is
edges is 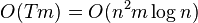 .
.
Karger–Stein algorithm
An extension of Karger’s algorithm due to David Karger and Clifford Stein achieves an order of magnitude improvement.[4]
The basic idea is to perform the contraction procedure until the graph reaches  vertices.
vertices.
procedure contract(,
): while
choose
uniformly at random
return
The probability 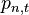 that this contraction procedure avoids a specific cut
that this contraction procedure avoids a specific cut  in an
in an  -vertex graph is
-vertex graph is
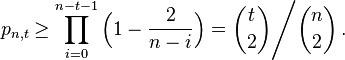
This expression is 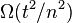 becomes less than
becomes less than  around
around 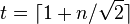 .
In particular, the probability that an edge from
.
In particular, the probability that an edge from  is contracted grows towards the end. This motivates the idea of switching to a slower algorithm after a certain number of contraction steps.
is contracted grows towards the end. This motivates the idea of switching to a slower algorithm after a certain number of contraction steps.
procedure fastmincut(): if
: return mincut(
) else:
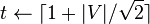
contract(
,
)
contract(
,
) return min {fastmincut(
), fastmincut(
)}
Analysis
The probability 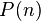 the algorithm finds a specific cutset
the algorithm finds a specific cutset  is given by the recurrence relation
is given by the recurrence relation
with solution 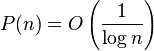 . The running time of fastmincut satisfies
. The running time of fastmincut satisfies
with solution 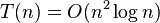 .
To achieve error probability
.
To achieve error probability 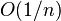 , the algorithm can be repeated
, the algorithm can be repeated 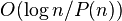 times, for an overall running time of
times, for an overall running time of 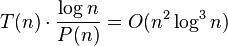 . This is an order of magnitude improvement over Karger’s original algorithm.
. This is an order of magnitude improvement over Karger’s original algorithm.
Finding all min-cuts
Theorem: With high probability we can find all min cuts in the running time of 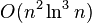 .
.
Proof: Since we know that 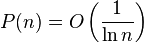 , therefore after running this algorithm
, therefore after running this algorithm 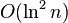 times The probability of missing a specific min-cut is
times The probability of missing a specific min-cut is
![\Pr[\text{miss a specific min-cut}] = (1-P(n))^{O(\ln ^2 n)} \le \left(1-\frac{c}{\ln n}\right)^{\frac{3\ln ^2 n}{c}} \le e^{-3\ln n} = \frac{1}{n^3}](../I/m/0f9b055373c65e569b6fb7317d520d88.png) .
.
And there are at most 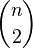 min-cuts, hence the probability of missing any min-cut is
min-cuts, hence the probability of missing any min-cut is
The probability of failures is considerably small when n is large enough.∎
Improvement bound
To determine a min-cut, one has to touch every edge in the graph at least once, which is 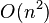 time in a dense graph. The Karger–Stein's min-cut algorithm takes the running time of
time in a dense graph. The Karger–Stein's min-cut algorithm takes the running time of 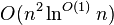 , which is very close to that.
, which is very close to that.
References
- ↑ 1.0 1.1 Karger, David (1993). "Global Min-cuts in RNC and Other Ramifications of a Simple Mincut Algorithm". Proc. 4th Annual ACM-SIAM Symposium on Discrete Algorithms.
- ↑ Stoer, M.; Wagner, F. (1997). "A simple min-cut algorithm". Journal of the ACM 44 (4): 585. doi:10.1145/263867.263872.
- ↑ Patrignani, Maurizio; Pizzonia, Maurizio (2001), "The complexity of the matching-cut problem", in Brandstädt, Andreas; Le, Van Bang, Graph-Theoretic Concepts in Computer Science: 27th International Workshop, WG 2001, Boltenhagen, Germany, June 14ÔÇô16, 2001, Proceedings, Lecture Notes in Computer Science 2204, Berlin: Springer, pp. 284–295, doi:10.1007/3-540-45477-2_26, MR 1905640.
- ↑ Karger, David R.; Stein, Clifford (1996). "A new approach to the minimum cut problem". Journal of the ACM 43 (4): 601. doi:10.1145/234533.234534.
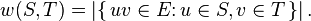

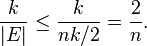
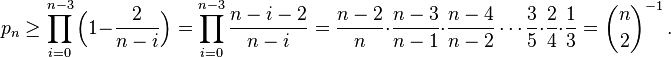
![\Bigl[1-\binom{n}{2}^{-1}\Bigr]^T
\leq \frac{1}{e^{\ln n}} = \frac{1}{n}\,.](../I/m/456f55faa05cd241db26883341c924ae.png)
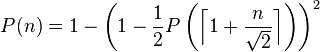
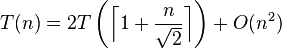
![\Pr[\text{miss any min-cut}] \le \binom{n}{2} \cdot \frac{1}{n^3} = O\left(\frac{1}{n}\right).](../I/m/197bd18c4dad2d5eec79b0d98fd6a0bc.png)