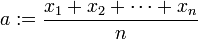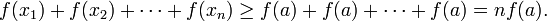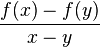Karamata's inequality

In mathematics, Karamata's inequality,^[1] named after Jovan Karamata,^[2] also known as the majorization inequality, is a theorem in elementary algebra for convex and concave real-valued functions, defined on an interval of the real line. It generalizes the discrete form of Jensen's inequality.

Statement of the inequality

Let $I$ be an interval of the real line and let $f$ denote a real-valued, convex function defined on $I$ . If $x 1, . . . , x n$ and $y 1, . . . , y n$ are numbers in $I$ such that $(x 1, . . . , x n)$ majorizes $(y 1, . . . , y n)$ , then

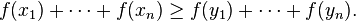
$f(x_1)+\cdots+f(x_n) \ge f(y_1)+\cdots+f(y_n).$

(1)

Here majorization means that

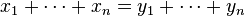
$x_1+\cdots+x_n=y_1+\cdots+y_n$

(2)

and, after relabeling the numbers $x 1, . . . , x n$ and $y 1, . . . , y n$ , respectively, in decreasing order, i.e.,

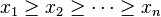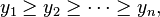
$x_1\ge x_2\ge\cdots\ge x_n$ and $y_1\ge y_2\ge\cdots\ge y_n,$

(3)

we have

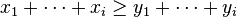$x_1+\cdots+x_i\ge y_1+\cdots+y_i$ for all $i \in {1, . . . , n - 1$ }.

(4)

If $f$ is a strictly convex function, then the inequality (1) holds with equality if and only if, after relabeling according to (3), we have $x i = y i$ for all $i \in {1, . . . , n$ }.

Remarks

If the convex function $f$ is non-decreasing, then the proof of (1) below and the discussion of equality in case of strict convexity shows that the equality (2) can be relaxed to

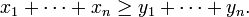
$x_1+\cdots+x_n\ge y_1+\cdots+y_n.$

(5)

The inequality (1) is reversed if $f$ is concave, since in this case the function $- f$ is convex.

Example

The finite form of Jensen's inequality is a special case of this result. Consider the real numbers $x 1, . . . , x n \in I$ and let

a := \frac{x_1+x_2+\cdots+x_n}{n}

denote their arithmetic mean. Then $(x 1, . . . , x n)$ majorizes the $n$ -tuple $(a, a, . . . , a)$ , since the arithmetic mean of the $i$ largest numbers of $(x 1, . . . , x n)$ is at least as large as the arithmetic mean $a$ of all the $n$ numbers, for every $i \in {1, . . . , n - 1$ }. By Karamata's inequality (1) for the convex function $f$ ,

f(x_1)+f(x_2)+ \cdots +f(x_n) \ge f(a)+f(a)+\cdots+f(a) = nf(a).

Dividing by $n$ gives Jensen's inequality. The sign is reversed if $f$ is concave.

Proof of the inequality

We may assume that the numbers are in decreasing order as specified in (3).

If $x i = y i$ for all $i \in {1, . . . , n$ }, then the inequality (1) holds with equality, hence we may assume in the following that $x i \neq y i$ for at least one $i$ .

If $x i = y i$ for an $i \in {1, . . . , n - 1$ }, then the inequality (1) and the majorization properties (2), (4) are not affected if we remove $x i$ and $y i$ . Hence we may assume that $x i \neq y i$ for all $i \in {1, . . . , n - 1$ }.

It is a property of convex functions that for two numbers $x \neq y$ in the interval $I$ the slope

\frac{f(x)-f(y)}{x-y}

of the secant line through the points $(x, f (x))$ and $(y, f (y))$ of the graph of $f$ is a monotonically non-decreasing function in $x$ for $y$ fixed (and vice versa). This implies that

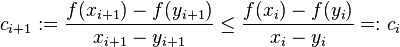
$c_{i+1}:=\frac{f(x_{i+1})-f(y_{i+1})}{x_{i+1}-y_{i+1}}\le\frac{f(x_i)-f(y_i)}{x_i-y_i}=:c_i$

(6)

for all $i \in {1, . . . , n - 1$ }. Define $A 0 = B 0 = 0$ and

A_i=x_1+\cdots+x_i,\qquad B_i=y_1+\cdots+y_i

for all $i \in {1, . . . , n$ }. By the majorization property (4), $A i \geq B i$ for all $i \in {1, . . . , n - 1$ } and by (2), $A n = B n$ . Hence,

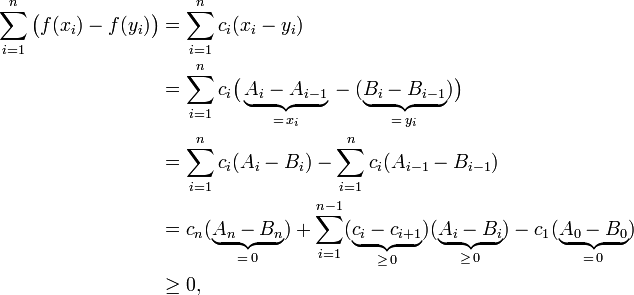
$\begin{align} \sum_{i=1}^n \bigl(f(x_i) - f(y_i)\bigr) &=\sum_{i=1}^n c_i (x_i - y_i)\\ &=\sum_{i=1}^n c_i \bigl(\underbrace{A_i - A_{i-1}}_{=\,x_i}{} - (\underbrace{B_i - B_{i-1}}_{=\,y_i})\bigr)\\ &=\sum_{i=1}^n c_i (A_i - B_i) - \sum_{i=1}^n c_i (A_{i-1} - B_{i-1})\\ &=c_n (\underbrace{A_n-B_n}_{=\,0}) + \sum_{i=1}^{n-1}(\underbrace{c_i - c_{i + 1}}_{\ge\,0})(\underbrace{A_i - B_i}_{\ge\,0}) - c_1(\underbrace{A_0-B_0}_{=\,0})\\ &\ge0, \end{align}$

(7)

which proves Karamata's inequality (1).

To discuss the case of equality in (1), note that $x 1 > y 1$ by (4) and our assumption $x i \neq y i$ for all $i \in {1, . . . , n - 1$ }. Let $i$ be the smallest index such that $(x i, y i) \neq (x i +1, y i +1)$ , which exists due to (2). Then $A i > B i$ . If $f$ is strictly convex, then there is strict inequality in (6), meaning that $c i +1 < c i$ . Hence there is a strictly positive term in the sum on the right hand side of (7) and equality in (1) cannot hold.

If the convex function $f$ is non-decreasing, then $c n \geq 0$ . The relaxed condition (5) means that $A n \geq B n$ , which is enough to conclude that $c n (A n - B n) \geq 0$ in the last step of (7).

If the function $f$ is strictly convex and non-decreasing, then $c n > 0$ . It only remains to discuss the case $A n > B n$ . However, then there is a strictly positive term on the right hand side of (7) and equality in (1) cannot hold.

References

↑ Kadelburg, Zoran; Đukić, Dušan; Lukić, Milivoje; Matić, Ivan (2005), "Inequalities of Karamata, Schur and Muirhead, and some applications", The Teaching of Mathematics 8 (1): 31–45, ISSN 1451-4966
↑ Karamata, Jovan (1932), "Sur une inégalité relative aux fonctions convexes", Publ. Math. Univ. Belgrade (in French) 1: 145–148, Zbl 0005.20101

External links

An explanation of Karamata's inequality and majorization theory can be found here.