K-theory spectrum

In mathematics, given a ring R, the K-theory spectrum of R is an Ω-spectrum 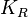K_R whose n-th term is given by, writing 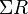\Sigma R for the suspension of R,

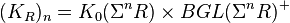(K_R)_n = K_0(\Sigma^n R) \times BGL(\Sigma^n R)^+,

where "+" means the Quillen's + construction.[1] By definition, 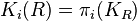K_i(R) = \pi_i(K_R).

References

  1. ↑ Dominique Arlettaz, Algebraic K-theory of rings from a topological view point