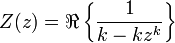K-noid

Trinoid
7-noid

In differential geometry, a k-noid is a minimal surface with k catenoid openings. In particular, the 3-noid is often called trinoid. The first k-noid minimal surfaces were described by Jorge and Meeks in 1983.[1]

The term k-noid and trinoid is also sometimes used for constant mean curvature surfaces, especially branched versions of the unduloid ("triunduloids").[2]

k-noids are topologically equivalent to k-punctured spheres (spheres with k points removed). k-noids with symmetric openings can be generated using the Weierstrass–Enneper parameterization 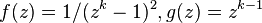f(z) = 1/(z^k-1)^2, g(z) = z^{k-1}\,\!.[3] This produces the explicit formula

\begin{align} X(z) = \frac{1}{2} \Re \Bigg\{ \Big(\frac{-1}{kz(z^k-1)} \Big) \Big[ &(k-1)(z^k-1)_2F_1(1,-1/k;(k-1)/k;z^k)\\ & {}-(k-1)z^2(z^k-1)_2F_1(1,1/k;1+1/k;z^k) \\ &{}-kz^k +k+z^2-1 \Big] \Bigg\} \end{align}
\begin{align} Y(z) = \frac{1}{2} \Re \Bigg\{ \Big(\frac{i}{kz(z^k-1)}\Big) \Big[ &(k-1)(z^k-1)_2F_1(1,-1/k;(k-1)/k;z^k) \\ &{}+(k-1)z^2(z^k-1)_2F_1(1,1/k;1+1/k;z^k)\\ & {}-kz^k+k-z^2-1 ) \Big] \Bigg\} \end{align}
Z(z) =\Re \left \{ \frac{1}{k-kz^k} \right\}

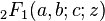where _2F_1(a,b;c;z) is the Gaussian hypergeometric function.

It is also possible to create k-noids with openings in different directions and sizes,[4] k-noids corresponding to the platonic solids and k-noids with handles.[5]

References

  1. ↑ L. P. Jorge and W. H. Meeks III, The topology of complete minimal surfaces of finite total Gaussian curvature, Topology 22 (1983)
  2. ↑ N Schmitt. "Constant Mean Curvature n-noids with Platonic Symmetries". Arxiv.org. Retrieved 2012-10-05.
  3. ↑ Matthias Weber (2001). "Classical Minimal Surfaces in Euclidean Space by Examples". Indiana.edu. Retrieved 2012-10-05.
  4. ↑ H. Karcher. "Construction of minimal surfaces, in "Surveys in Geometry", University of Tokyo, 1989, and Lecture Notes No. 12, SFB 256, Bonn, 1989, pp. 1-96". Math.uni-bonn-de. Retrieved 2012-10-05.
  5. ↑ Jorgen Berglund, Wayne Rossman. "Minimal Surfaces with Catenoid Ends. Pacific J. Math. Volume 171, Number 2 (1995),pp. 353-371". Arxiv.org. Retrieved 2012-10-05.

External links