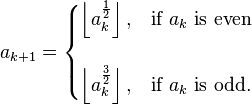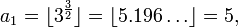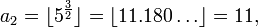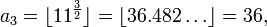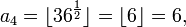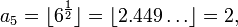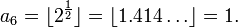Juggler sequence

In recreational mathematics a juggler sequence is an integer sequence that starts with a positive integer a0, with each subsequent term in the sequence defined by the recurrence relation:

a_{k+1}= \begin{cases} \left \lfloor a_k^{\frac{1}{2}} \right \rfloor, & \mbox{if } a_k \mbox{ is even} \\ \\ \left \lfloor a_k^{\frac{3}{2}} \right \rfloor, & \mbox{if } a_k \mbox{ is odd}. \end{cases}

Background

Juggler sequences were publicised by American mathematician and author Clifford A. Pickover.[1] The name is derived from the rising and falling nature of the sequences, like balls in the hands of a juggler.[2]

For example, the juggler sequence starting with a0 = 3 is

a_1= \lfloor 3^\frac{3}{2} \rfloor = \lfloor 5.196\dots \rfloor = 5,
a_2= \lfloor 5^\frac{3}{2} \rfloor = \lfloor 11.180\dots \rfloor = 11,
a_3= \lfloor 11^\frac{3}{2} \rfloor = \lfloor 36.482\dots \rfloor = 36,
a_4= \lfloor 36^\frac{1}{2} \rfloor = \lfloor 6 \rfloor = 6,
a_5= \lfloor 6^\frac{1}{2} \rfloor = \lfloor 2.449\dots \rfloor = 2,
a_6= \lfloor 2^\frac{1}{2} \rfloor = \lfloor 1.414\dots \rfloor = 1.

If a juggler sequence reaches 1, then all subsequent terms are equal to 1. It is conjectured that all juggler sequences eventually reach 1. This conjecture has been verified for initial terms up to 106,[3] but has not been proved. Juggler sequences therefore present a problem that is similar to the Collatz conjecture, about which Paul Erdős stated that "mathematics is not yet ready for such problems".

For a given initial term n, one defines l(n) to be the number of steps which the juggler sequence starting at n takes to first reach 1, and h(n) to be the maximum value in the juggler sequence starting at n. For small values of n we have:

n Juggler sequence l(n)

(sequence A007320 in OEIS)

 h(n)

(sequence A094716 in OEIS)

2 2, 1 1 2
3 3, 5, 11, 36, 6, 2, 1 6 36
4 4, 2, 1 2 4
5 5, 11, 36, 6, 2, 1 5 36
6 6, 2, 1 2 6
7 7, 18, 4, 2, 1 4 18
8 8, 2, 1 2 8
9 9, 27, 140, 11, 36, 6, 2, 1 7 140
10 10, 3, 5, 11, 36, 6, 2, 1 7 36

Juggler sequences can reach very large values before descending to 1. For example, the juggler sequence starting at a0 = 37 reaches a maximum value of 24906114455136. Harry J. Smith has determined that the juggler sequence starting at a0 = 48443 reaches a maximum value at a60 with 972,463 digits, before reaching 1 at a157.[4]

References

  1. ↑ Pickover, Clifford A. (1992). Computers and the Imagination. St. Martin's Press. pp. Chapter 40. ISBN 978-0-312-08343-4.
  2. ↑ Pickover, Clifford A. (2002). The Mathematics of Oz. Cambridge University Press. pp. Chapter 45. ISBN 978-0-521-01678-0.
  3. ↑
  4. ↑ Letter from Harry J. Smith to Cliiford A. Pickover, 27 June 1992

External links