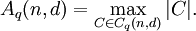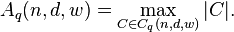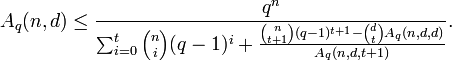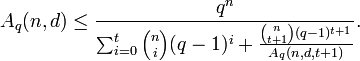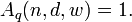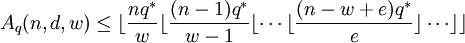Johnson bound
The Johnson bound is a limit on the size of error-correcting codes, as used in coding theory for data transmission or communications.
Definition
Let  be a q-ary code of length
be a q-ary code of length  , i.e. a subset of
, i.e. a subset of 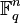 . Let
. Let  be the minimum distance of
be the minimum distance of  , i.e.
, i.e.
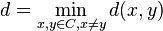 ,
,
where 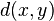 is the Hamming distance between
is the Hamming distance between  and
and  .
.
Let 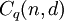 be the set of all q-ary codes with length
be the set of all q-ary codes with length  and minimum distance
and minimum distance  and let
and let 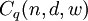 denote the set of codes in
denote the set of codes in 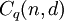 such that every element has exactly
such that every element has exactly 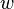 nonzero entries.
nonzero entries.
Denote by 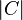 the number of elements in
the number of elements in  . Then, we define
. Then, we define 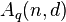 to be the largest size of a code with length
to be the largest size of a code with length  and minimum distance
and minimum distance  :
:
Similarly, we define 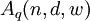 to be the largest size of a code in
to be the largest size of a code in 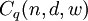 :
:
Theorem 1 (Johnson bound for 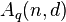 ):
):
If 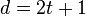 ,
,
If 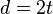 ,
,
Theorem 2 (Johnson bound for 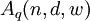 ):
):
(i) If 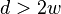 ,
,
(ii) If 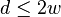 , then define the variable
, then define the variable  as follows. If
as follows. If  is even, then define
is even, then define  through the relation
through the relation 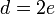 ; if
; if  is odd, define
is odd, define  through the relation
through the relation 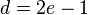 . Let
. Let 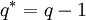 . Then,
. Then,
where  is the floor function.
is the floor function.
Remark: Plugging the bound of Theorem 2 into the bound of Theorem 1 produces a numerical upper bound on 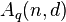 .
.
See also
- Singleton bound
- Hamming bound
- Plotkin bound
- Elias Bassalygo bound
- Gilbert–Varshamov bound
- Griesmer bound
References
- S. M. Johnson, "A new upper bound for error-correcting codes," IRE Transactions on Information Theory, pp. 203–207, April 1962.
- W. Cary Huffman, Vera Pless, Fundamentals of Error-Correcting Codes, Cambridge University Press, 2003.