Jenny Harrison

Jenny Harrison is a professor of mathematics at UC Berkeley. She specializes in geometric analysis and areas in the intersection of algebra, geometry, and geometric measure theory. She introduced and developed with collaborators a theory of generalized functions called differential chains[1][2] that unifies an infinitesimal calculus with the classical theory of the smooth continuum, a long outstanding problem. The infinitesimals are constructive and arise from methods of standard analysis, as opposed to the nonstandard analysis of Abraham Robinson. The methods apply equally well to domains such as soap films, fractals, charged particles, and Whitney stratified spaces, placing them on the same footing as smooth submanifolds in the resulting calculus. The results include optimal generalizations and simplifications of the theorems of Stokes, Gauss and Green. She has pioneered applications of differential chains to the calculus of variations, physics, and continuum mechanics. Her solution to Plateau's problem[3] is the first proof of existence of a solution to a universal Plateau’s problem for finitely many boundary curves, taking into account all soap films arising in nature, including nonorientable films with triple junctions, as well as solutions of Jesse Douglas,[4] Herbert Federer and Wendell Fleming.[5] Recently, she and Harrison Pugh have announced existence and soap film regularity of a solution to a universal Plateau's problem for codimension one surfaces using Hausdorff measure to define area.
Harrison grew up in Tuscaloosa, Alabama. Her graduate studies were at the University of Warwick, where her adviser E.C. Zeeman introduced her to Plateau's problem. Hassler Whitney was her postdoctoral adviser at the Institute for Advanced Study. She found a counterexample to the Seifert conjecture[6] while on the faculty at Oxford University. In a Berkeley seminar in 1983 she proposed the existence of a general theory linking these together, and the theory of differential chains began to evolve. Jenny Harrison and Harrison Pugh proved that the topological vector space of differential chains satisfies a universal property determined by two natural axioms.[2] They have used the theory to provide the first universal solution to Plateau's problem, including soap film regularity, building upon Harrison's earlier paper.[7] Recently, Fried and Seguin have found a broad generalization to Reynolds transport theorem using the methods of differential chains.[8]
Gender discrimination lawsuit
Harrison initiated a lawsuit based on gender discrimination in the 1986 tenure decision by the Berkeley mathematics department. The case attracted international attention. The 1993 settlement led to a new review of her work by a panel of seven mathematicians and science faculty who unanimously recommended tenure as a full professor. The review included her generalization of Stokes' theorem to nonsmooth domains. Stephen Smale and Robion Kirby were the most vocal opponents to her receiving tenure during the case, while Morris Hirsch and James Yorke were her most vocal supporters.
Awards and Fellowships
- Foundational Questions Institute, research award, 2009
- Miller Institute for Basic Research in Science, Miller Professor, 2007
- Rockefeller University, Visiting Research Professor, 1996–97
- Yale University, National Science Foundation, Visiting Scholar, 1989–90
- Oxford University, CUF Lecturer and Tutorial Fellow, Somerville College, 1978–81
- Miller Institute for Basic Research in Science, Miller Fellow, 1977–78
- Institute for Advanced Study, Visiting Fellow, Princeton, 1975–76
References
- ↑ Jenny Harrison, Operator calculus of differential chains and differential forms, to appear in the Journal of Geometric Analysis, arxiv posting January 2011, 89 pages
- ↑ 2.0 2.1 J. Harrison and H. Pugh, Topological Aspects of Differential Chains, Journal of Geometric Analysis, 22 (2012), no. 3, 685–690
- ↑ Jenny Harrison, Soap film solutions to Plateau's problem, Journal of Geometric Analysis, January 2014, 24(1):271-2972
- ↑ Jesse Douglas, Solutions of the problem of Plateau, Transactions of the American Mathematical Society 33 (1931), 263–321
- ↑ Herbert Federer and Wendell Fleming, Normal and integral currents, The Annals of Mathematics 72 (1960), no. 3, 458–520
- ↑ Jenny Harrison,
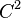 counterexamples to the Seifert conjecture. Topology (journal)|Topology, vol. 27, no. 3, pp. 249–278, 1988
counterexamples to the Seifert conjecture. Topology (journal)|Topology, vol. 27, no. 3, pp. 249–278, 1988 - ↑ Jenny Harrison, Journal of Geometric Analysis, January 2013, 24(1):271-297
- ↑ Eliot Fried and Brian Seguin, Mathematical Models and Methods in Applied Sciences, Vol. 24, No. 9 (2014) 1729–1779