Jacobson's conjecture
In abstract algebra, Jacobson's conjecture is an open problem in ring theory concerning the intersection of powers of the Jacobson radical of a Noetherian ring.
It has only been proven for special types of Noetherian rings, so far. Examples exist to show that the conjecture can fail when the ring is not Noetherian on a side, so it is absolutely necessary for the ring to be two-sided Noetherian.
The conjecture is named for the algebraist Nathan Jacobson who posed the first version of the conjecture.
Statement
For a ring R with Jacobson radical J, the nonnegative powers Jn are defined by using the product of ideals.
- Jacobson's conjecture: In a right-and-left Noetherian ring,
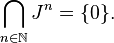
In other words: "The only element of a Noetherian ring in all powers of J is 0."
The original conjecture posed by Jacobson in 1956[1] asked about noncommutative one-sided Noetherian rings, however Herstein produced a counterexample in 1965[2] and soon after Jategaonkar produced a different example which was a left principal ideal domain.[3] From that point on, the conjecture was reformulated to require two-sided Noetherian rings.
Partial results
Jacobson's conjecture has been verified for particular types of Noetherian rings:
- Commutative Noetherian rings all satisfy Jacobson's conjecture. This is a consequence of the Krull intersection theorem.
- Fully bounded Noetherian rings[4][5]
- Noetherian rings with Krull dimension 1[6]
- Noetherian rings satisfying the second layer condition[7]
References
- ↑ Jacobson, Nathan (1956), Structure of rings, American Mathematical Society, Colloquium Publications, vol. 37, 190 Hope Street, Prov., R. I.: American Mathematical Society, p. 200, MR 0081264. As cited by Brown, K. A.; Lenagan, T. H. (1982), "A note on Jacobson's conjecture for right Noetherian rings", Glasgow Mathematical Journal 23 (1): 7–8, doi:10.1017/S0017089500004729, MR 641612.
- ↑ Herstein 1965.
- ↑ Jategaonkar 1968.
- ↑ Cauchon 1974.
- ↑ Jategaonkar 1974.
- ↑ Lenagan 1977.
- ↑ Jategaonkar 1982.
- Cauchon, Gérard (1974), "Sur l'intersection des puissances du radical d'un T-anneau noethérien", C. R. Acad. Sci. Paris Sér. A (in French) 279: 91–93, MR 0347894
- Goodearl, K. R.; Warfield, R. B., Jr. (2004), An introduction to noncommutative Noetherian rings, London Mathematical Society Student Texts 61 (2 ed.), Cambridge: Cambridge University Press, pp. xxiv+344, ISBN 0-521-54537-4, MR 2080008
- Herstein, I. N. (1965), "A counterexample in Noetherian rings", Proc. Nat. Acad. Sci. U.S.A. 54: 1036–1037, doi:10.1073/pnas.54.4.1036, ISSN 0027-8424, MR 0188253
- Jategaonkar, Arun Vinayak (1968), "Left principal ideal domains", J. Algebra 8: 148–155, doi:10.1016/0021-8693(68)90040-9, ISSN 0021-8693, MR 0218387
- Jategaonkar, Arun Vinayak (1974), "Jacobson's conjecture and modules over fully bounded Noetherian rings", J. Algebra 30: 103–121, doi:10.1016/0021-8693(74)90195-1, ISSN 0021-8693, MR 0352170
- Jategaonkar, Arun Vinayak (1982), "Solvable Lie algebras, polycyclic-by-finite groups and bimodule Krull dimension", Comm. Algebra 10 (1): 19–69, doi:10.1080/00927878208822700, ISSN 0092-7872, MR 674687
- Lenagan, T. H. (1977), "Noetherian rings with Krull dimension one", J. London Math. Soc. (2) 15 (1): 41–47, ISSN 0024-6107, MR 0442008
- Rowen, Louis H. (1988), Ring theory. Vol. I, Pure and Applied Mathematics 127, Boston, MA: Academic Press Inc., pp. xxiv+538, ISBN 0-12-599841-4, MR 940245