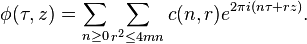Jacobi form

In mathematics, a Jacobi form is an automorphic form on the Jacobi group, which is the semidirect product of the symplectic group Sp(n;R) and the Heisenberg group $H^{(n,h)}_R$ . The theory was first systematically studied by Eichler & Zagier (1985).

Definition

A Jacobi form of level 1, weight k and index m is a function φ(τ,z) of two complex variables (with τ in the upper half plane) such that

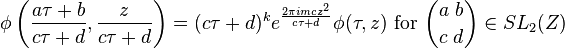
$\phi\left(\frac{a\tau+b}{c\tau+d},\frac{z}{c\tau+d}\right) = (c\tau+d)^ke^{\frac{2\pi i mcz^2}{c\tau+d}}\phi(\tau,z)\text{ for }{a\ b\choose c\ d}\in SL_2(Z)$
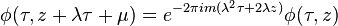$\phi(\tau,z+\lambda\tau+\mu) = e^{-2\pi i m(\lambda^2\tau+2\lambda z)}\phi(\tau,z)$ for all integers λ μ.
$\phi$ has a Fourier expansion

\phi(\tau,z) = \sum_{n\ge 0} \sum_{r^2\le 4mn} c(n,r)e^{2\pi i (n\tau+rz)}.

Examples

Examples in two variables include Jacobi theta functions, the Weierstrass ℘ function, and Fourier–Jacobi coefficients of Siegel modular forms of genus 2. Examples with more than two variables include characters of some irreducible highest-weight representations of affine Kac–Moody algebras. Meromorphic Jacobi forms appear in the theory of Mock modular forms.

References

Eichler, Martin; Zagier, Don (1985), The theory of Jacobi forms, Progress in Mathematics 55, Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-3180-2, MR 781735