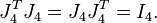Jacket matrix

In mathematics, a jacket matrix is a square matrix 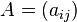A= (a_{ij}) of order n if its entries are non-zero and real, complex, or from a finite field, and

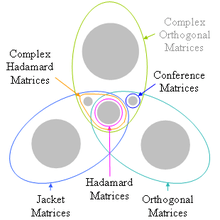
Hierarchy of matrix types
\ AB=BA=I_n

where In is the identity matrix, and

\ B ={1 \over n}(a_{ij}^{-1})^T.

where T denotes the transpose of the matrix.

In other words, the inverse of a jacket matrix is determined its element-wise or block-wise inverse. The definition above may also be expressed as:

\forall u,v \in \{1,2,\dots,n\}:~a_{iu},a_{iv} \neq 0, ~~~~ \sum_{i=1}^n a_{iu}^{-1}\,a_{iv} = \begin{cases} n, & u = v\\ 0, & u \neq v \end{cases}

The jacket matrix is a generalization of the Hadamard matrix,also it is a Diagonal block-wise inverse matrix.

Motivation

n .... -2, -1, 0 1, 2,..... logarithm
2^n ....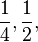\ {1 \over 4},{1 \over 2}, 1, 2, 4,..... Series

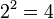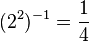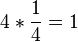As shown in Table, i.e. in series, n=2 case, Forward: 2^2=4 , Inverse  : (2^2)^{-1}={1 \over 4} , then, 4*{1\over 4}=1.

Therefore, exist an element-wise inverse.

Example 1.

A = \left[ \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & -2 & 2 & -1 \\ 1 & 2 & -2 & -1 \\ 1 & -1 & -1 & 1 \\ \end{array} \right],:B ={1 \over 4} \left[ \begin{array}{rrrr} 1 & 1 & 1 & 1 \\[6pt] 1 & -{1 \over 2} & {1 \over 2} & -1 \\[6pt] 1 & {1 \over 2} & -{1 \over 2} & -1 \\[6pt] 1 & -1 & -1 & 1\\[6pt] \end{array} \right].

or more general

A = \left[ \begin{array}{rrrr} a & b & b & a \\ b & -c & c & -b \\ b & c & -c & -b \\ a & -b & -b & a \end{array} \right], : B = {1 \over 4} \left[ \begin{array}{rrrr} {1 \over a} & {1 \over b} & {1 \over b} & {1 \over a} \\[6pt] {1 \over b} & -{1 \over c} & {1 \over c} & -{1 \over b} \\[6pt] {1 \over b} & {1 \over c} & -{1 \over c} & -{1 \over b} \\[6pt] {1 \over a} & -{1 \over b} & -{1 \over b} & {1 \over a} \end{array} \right],

Example 2.

For m x m matrices, 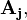\mathbf {A_j},

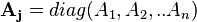\mathbf {A_j}=diag(A_1, A_2,.. A_n ) denotes an mn x mn block diagonal Jacket matrix.

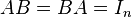
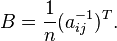
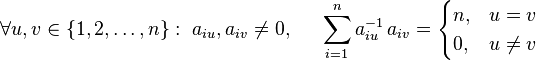
J_4 = \left[ \begin{array}{rrrr} I_2 & 0 & 0 & 0 \\ 0 & cos\theta & -sin\theta & 0 \\ 0 & sin\theta & cos\theta & 0 \\ 0 & 0 & 0 & I_2 \end{array} \right], \ J^T_4 J_4 =J_4 J^T_4=I_4.

References

External links