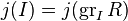j-multiplicity

In algebra, a j-multiplicity is a generalization of a Hilbert–Samuel multiplicity. For m-primary ideals, the two notions coincide.

Definition

Let 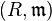$(R, \mathfrak{m})$ be a local Noetherian ring of Krull dimension 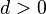$d > 0$ . Then the j-multiplicity of an ideal I is

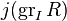j(I) = j(\operatorname{gr}_I R)

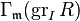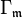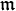where $j(\operatorname{gr}_I R)$ is the normalized coefficient of the degree d − 1 term in the Hilbert polynomial $\Gamma_\mathfrak{m}(\operatorname{gr}_I R)$ ; $\Gamma_\mathfrak{m}$ means the space of sections supported at $\mathfrak{m}$ .

References

Daniel Katz, Javid Validashti, Multiplicities and Rees valuations
Katz, Daniel; Validashti, Javid (2010). "Multiplicities and Rees valuations". Collectanea Mathematica 61: 1–24. doi:10.1007/BF03191222. Zbl 1216.13016.